Von WEIERSTRASS sind die Funktionen
 |
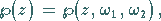(14.114a) |
 |
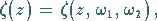(14.114b) |
 |
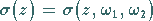(14.114c) |
eingeführt worden, wobei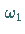 
und 
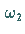zwei beliebige komplexe Zahlen
darstellen, deren Quotient nicht reell ist.
Man setzt
 |
(14.115a) |
wobei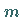 
und 
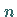beliebige ganze Zahlen sind, und definiert
 |
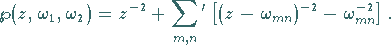(14.115b) |
Dabei deutet der Strich am Summenzeichen an, daß das Wertepaar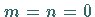 
ausgenommen
ist.
Die Funktion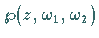 
hat folgende Eigenschaften:
1. Sie ist eine elliptische Funktion mit den Perioden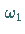
und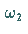 
.
2. Die Reihe (14.115b) konvergiert für alle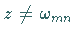 
.
3. Die Funktion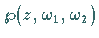
genügt der Differentialgleichung
 |
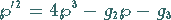(14.116a) |
mit
 |
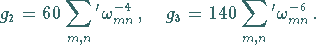(14.116b) |
Die Größen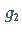 
und 
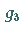werden als Invarianten von
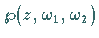bezeichnet.
4. Die Funktion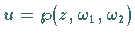 
ist die Umkehrfunktion zu dem Integral
 |
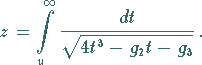(14.117) |
5.
 |
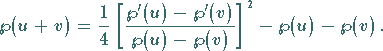(14.118) |
Die WEIERSTRASSschen Funktionen
 |
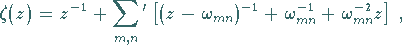(14.119a) |
 |
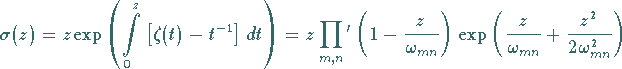(14.119b) |
sind nicht doppelperiodisch, also keine elliptischen Funktionen.
Es gelten folgende Beziehungen:
1.
 |
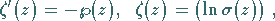(14.120) |
2.
 |
(14.121) |
3.
 |
(14.122) |
4.
 |
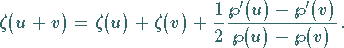(14.123) |
5. Jede elliptische Funktion ist eine rationale Funktion der
WEIERSTRASSschen Funktionen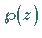 
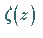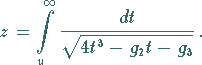
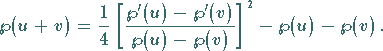
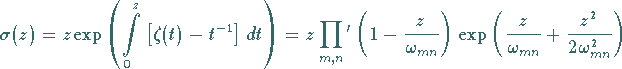
und 
.
