Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        


Zusammenhang mit elliptischen Integralen

Integrale der Form (8.20a,b), mit dem Integranden , lassen sich, abgesehen von Ausnahmefällen, nicht in geschlossener Form integrieren, wenn ein Polynom dritten oder vierten Grades ist, sondern sind als elliptische Integrale numerisch zu berechnen. Die Umkehrfunktionen der elliptischen Integrale sind die elliptischen Funktionen . Sie sind den trigonometrischen Funktionen ähnlich und können als deren Verallgemeinerung angesehen werden. Um das am speziellen Fall zu zeigen, wird
(14.98)

gesetzt und beachtet, daß
a) zwischen der trigonometrischen Funktion und dem Hauptwert ihrer Umkehrfunktion der Zusammenhang
(14.99)

besteht und daß
b) das Integral (14.98) gleich ist. Die Sinusfunktion kann somit als Umkehrfunktion des Integrals (14.98) aufgefaßt werden. Analoges gilt für die elliptischen Integrale.

Beispiel

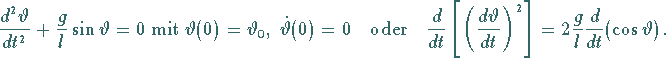Die Schwingungsdauer des mathematischen Pendels mit der an einem masselosen nicht dehnbaren Faden der Länge befestigten Masse (s. Abbildung) kann mit Hilfe einer nichtlinearen Differentialgleichung 2. Ordnung, die sich als Bewegungsgleichung aus dem Gleichgewicht der an der Masse angreifenden Kräfte ergibt, berechnet werden:


(14.100a)

Zwischen Pendellänge und Auslenkung aus der Ruhelage besteht der Zusammenhang , also und . Die an der Masse angreifende Kraft , wobei die Fallbeschleunigung ist, spaltet, bezogen auf die Bahnkurve, in eine Normalkomponente und eine Tangentialkomponente auf (s. obige Abbildung). Die Normalkomponente wird von der Fadenspannung im Gleichgewicht gehalten. Da sie senkrecht auf der Bewegungsrichtung steht, liefert sie keinen Beitrag zur Bewegungsgleichung. Die Tangentialkomponente steht mit der entgegengesetzt gleich großen Tangentialkraft im Gleichgewicht: . Die Tangentialkomponente zeigt immer zur Ruhelage hin.
Durch Trennung der Variablen erhält man die Pendelgleichung

(14.100b)

Dabei bedeutet die Zeit, bei der das Pendel zum ersten Mal durch die tiefste Lage geht, d.h., es gilt . Mit ist die Integrationsvariable bezeichnet. Aus (14.100b) erhält man nach einigen Umformungen mit Hilfe der Substitution
(14.100c)

die Gleichung
(14.100d)

Dabei ist ein elliptisches Integral 1. Gattung. Der Ausschlagwinkel ist eine periodische Funktion der Periode mit
(14.100e)

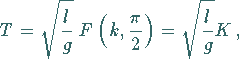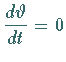wobei ein vollständiges elliptisches Integral 1. Gattung darstellt (s.  auch Tabelle). Mit ist die Schwingungsdauer des Pendels bezeichnet, d.h. die Zeit zwischen zwei Umkehrpunkten, für die gilt. Für kleine Auslenkungen mit wird .