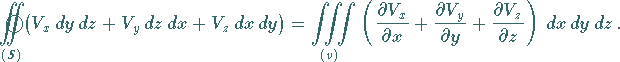Integralsatz von Gauß
Der Integralsatz von GAUSS liefert den Zusammenhang zwischen einem
Volumenintegral über ein Volumen 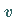 ,
das von einem Feld
,
das von einem Feld 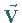 durchsetzt ist,
und einem Oberflächenintegral über die dieses Volumen umschließende Fläche
durchsetzt ist,
und einem Oberflächenintegral über die dieses Volumen umschließende Fläche
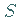 .
Die Orientierung der Fläche sei so festgelegt, daß die
Außenseite die positive Seite ist.
Die vektorielle Feldfunktion
.
Die Orientierung der Fläche sei so festgelegt, daß die
Außenseite die positive Seite ist.
Die vektorielle Feldfunktion 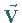 soll stetig sein, ihre ersten partiellen
Ableitungen sollen existieren und stetig sein.
soll stetig sein, ihre ersten partiellen
Ableitungen sollen existieren und stetig sein.
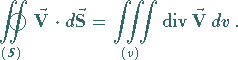 |
(13.117a) |
Der skalare Fluß des Feldes 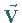 durch die geschlossene Fläche
durch die geschlossene Fläche 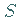 ist
gleich dem Integral der Divergenz von
ist
gleich dem Integral der Divergenz von 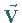 über das von
über das von 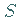 umschlossene
Volumen
umschlossene
Volumen 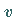 .
In kartesischen Koordinaten gilt:
.
In kartesischen Koordinaten gilt:
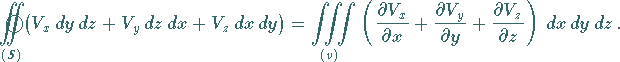 |
(13.117b) |
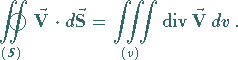
![]() durch die geschlossene Fläche
durch die geschlossene Fläche ![]() ist
gleich dem Integral der Divergenz von
ist
gleich dem Integral der Divergenz von ![]() über das von
über das von ![]() umschlossene
Volumen
umschlossene
Volumen ![]() .
In kartesischen Koordinaten gilt:
.
In kartesischen Koordinaten gilt: