Richtungsableitung eines skalaren Feldes
Die Richtungsableitung des skalaren Feldes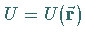 
in einem Punkt 
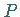mit dem Ortsvektor 
nach einem Vektor 
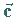(s. Abbildung)
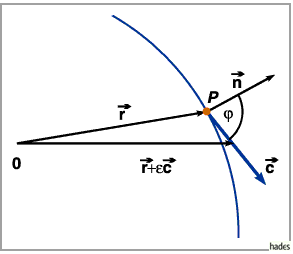
ist definiert als Grenzwert des Quotienten
 |
(13.27) |
Wenn die Ableitung des Feldes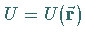
in einem Punkt
nach der
Richtung des Einheitsvektors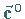 
von
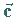mit
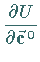bezeichnet wird, dann besteht
zwischen den Ableitungen der Funktion nach dem Vektor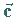
und nach seinem
Einheitsvektor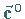
in ein und demselben Punkt die Beziehung
 |
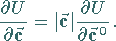(13.28) |
Die Ableitung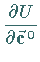
nach dem Einheitsvektor
ist ein Maß für die Stärke, mit der die Funktion 
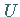in Richtung
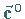vom Punkt
aus anwächst.
Unter allen Ableitungen in einem Punkt nach den verschiedenen Richtungen der
Einheitsvektoren besitzt die Ableitung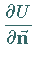 
den
größten Wert.
Dabei ist 
der Normaleneinheitsvektor zur Niveaufläche, auf der der Punkt
liegt.
Zwischen den Richtungsableitungen bezüglich
und einer beliebigen Richtung
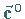besteht der Zusammenhang
 |
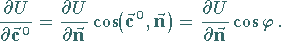(13.29) |
