Resolventenmenge und Resolvente eines Operators
Bei Untersuchungen zur Lösbarkeit von Gleichungen ist man bestrebt, das Problem auf die
Form
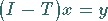 |
(12.149) |
mit einem Operator  von möglichst kleiner Norm zu bringen, da diese wegen
(12.139) und (12.140) für eine
funktionalanalytische Behandlung besonders zugänglich ist.
Um mit der Theorie auch große Werte von
von möglichst kleiner Norm zu bringen, da diese wegen
(12.139) und (12.140) für eine
funktionalanalytische Behandlung besonders zugänglich ist.
Um mit der Theorie auch große Werte von 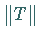 zu erfassen, untersucht man in einem
komplexen BANACH-Raum
zu erfassen, untersucht man in einem
komplexen BANACH-Raum  die gesamte Schar von Gleichungen
die gesamte Schar von Gleichungen
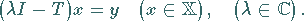 |
(12.150) |
Sei  ein linearer, im allgemeinen unbeschränkter Operator im BANACH-Raum
ein linearer, im allgemeinen unbeschränkter Operator im BANACH-Raum  .
Die Menge
.
Die Menge 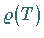 aller komplexen Zahlen, für die
aller komplexen Zahlen, für die
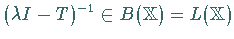 gilt, heißt Resolventenmenge und der
Operator
gilt, heißt Resolventenmenge und der
Operator 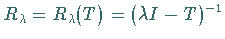 Resolvente .
Sei jetzt
Resolvente .
Sei jetzt  ein beschränkter linearer Operator in einem komplexen BANACH-Raum
ein beschränkter linearer Operator in einem komplexen BANACH-Raum
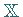 .
Dann gelten die Aussagen:
.
Dann gelten die Aussagen:
1. Die Menge 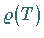 ist offen. Genauer, ist
ist offen. Genauer, ist 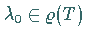 und genügt
und genügt 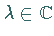 der Ungleichung
der Ungleichung
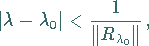 |
(12.151) |
dann existiert 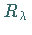 ,
und es gilt
,
und es gilt
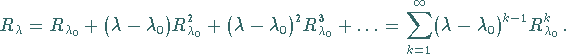 |
(12.152) |
2. 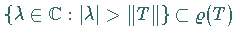 .
Genauer, für
.
Genauer, für
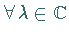 mit
mit 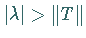 existiert
existiert 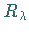 und
und
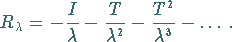 |
(12.153) |
3. 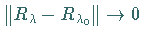 ,
wenn
,
wenn
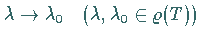 ,
und
,
und
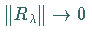 ,
wenn
,
wenn
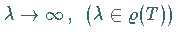 .
.
4. 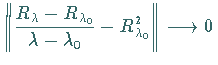 ,
wenn
,
wenn 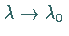 .
.
5. Für ein beliebiges Funktional 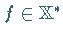 und beliebiges
und beliebiges 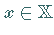 ist
ist
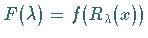 eine holomorphe Funktion auf
eine holomorphe Funktion auf 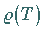 .
.
6. Für beliebige 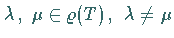 gilt
gilt
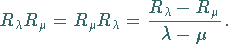 |
(12.154) |
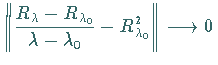 ,
wenn
,
wenn