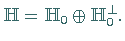Eigenschaften der Orthogonalität
Der Nullvektor ist zu jedem Vektor aus 
orthogonal.
Es gilt:
a) 
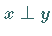und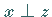 
impliziert 
.
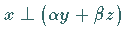b) Aus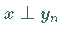 
und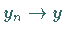 
folgt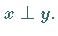 
c)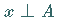 
genau dann, wenn 
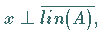wobei
die abgeschlossene lineare Hülle der Menge 
bezeichnet.
d) Ist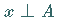
und
eine fundamentale Menge, d.h.,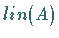 
ist
überall dicht in 
,
dann ist 
.
e) Satz des Pythagoras: Sind die Elemente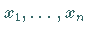 
paarweise orthogonal, also 
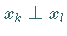für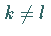 
,
dann ist
 |
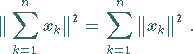(12.113) |
f) Projektionssatz: Ist 
ein Teilraum von ,
dann ist jeder Vektor
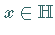eindeutig in der Form
 |
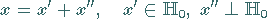(12.114) |
darstellbar.
g) Approximationsproblem: Weiter gilt
,
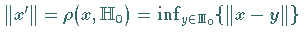so daß
 |
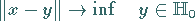(12.115) |
in
mit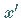 
eindeutig lösbar ist.
kann dabei sogar durch eine konvexe, abgeschlossene nichtleere Teilmenge aus
ersetzt werden.
Das Element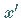
heißt Projektion des Elements 
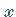auf 
,
besitzt den
kleinsten Abstand von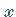
(zu ), und der Raum
ist orthogonal zerlegbar:
