In einem normierten Raum kann man Reihen von Elementen
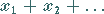 |
(12.85) |
betrachten.
Eine Reihe heißt konvergent , wenn die Folge der Partialsummen einen Grenzwert
besitzt:
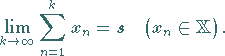 |
(12.86) |
Der Grenzwert 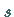 heißt dann Summe der Reihe, wofür man auch
heißt dann Summe der Reihe, wofür man auch
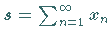 schreibt.
Eine Reihe
schreibt.
Eine Reihe 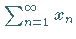 heißt absolut konvergent , wenn die
Zahlenreihe
heißt absolut konvergent , wenn die
Zahlenreihe 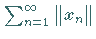 konvergiert.
Im BANACH-Raum ist jede absolut konvergente Reihe konvergent, wobei für ihre
Summe
konvergiert.
Im BANACH-Raum ist jede absolut konvergente Reihe konvergent, wobei für ihre
Summe 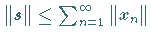 gilt.
gilt.