Ordnungsbeschränkte Mengen
Sei 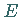 eine beliebige nichtleere Menge eines geordneten Vektorraumes
eine beliebige nichtleere Menge eines geordneten Vektorraumes 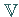 .
Ein Element
.
Ein Element 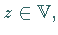 für das
für das 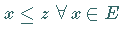 gilt, heißt
obere Schranke der Menge
gilt, heißt
obere Schranke der Menge 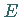 .
Eine untere Schranke für
.
Eine untere Schranke für 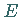 ist ein Element
ist ein Element 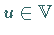 mit
Für zwei Elemente
mit
Für zwei Elemente 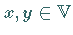 mit
mit 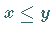 definiert man die Menge
definiert man die Menge
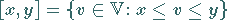 |
(12.31) |
und nennt sie Ordnungsintervall oder 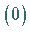 - Intervall .
Offenbar sind
- Intervall .
Offenbar sind 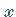 bzw.
bzw. 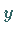 untere bzw. obere Schranke der Menge
untere bzw. obere Schranke der Menge 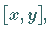 wobei diese der
Menge sogar angehören.
Eine Menge
wobei diese der
Menge sogar angehören.
Eine Menge 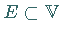 heißt nun ordnungs- oder einfach
(0)- beschränkt, wenn
heißt nun ordnungs- oder einfach
(0)- beschränkt, wenn 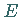 Teilmenge eines Ordnungsintervalls ist, d.h., wenn zwei
Elemente
Teilmenge eines Ordnungsintervalls ist, d.h., wenn zwei
Elemente 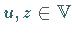 existieren, so daß
existieren, so daß 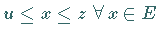 oder, was äquivalent dazu ist,
oder, was äquivalent dazu ist, 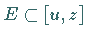 gilt.
Eine von oben beschränkte bzw. von unten beschränkte Menge ist eine Menge,
für die eine obere bzw. eine untere Schranke in
gilt.
Eine von oben beschränkte bzw. von unten beschränkte Menge ist eine Menge,
für die eine obere bzw. eine untere Schranke in 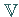 existiert.
existiert.
![]() - Intervall .
Offenbar sind
- Intervall .
Offenbar sind ![]() bzw.
bzw. ![]() untere bzw. obere Schranke der Menge
untere bzw. obere Schranke der Menge ![]() wobei diese der
Menge sogar angehören.
Eine Menge
wobei diese der
Menge sogar angehören.
Eine Menge ![]() heißt nun ordnungs- oder einfach
(0)- beschränkt, wenn
heißt nun ordnungs- oder einfach
(0)- beschränkt, wenn ![]() Teilmenge eines Ordnungsintervalls ist, d.h., wenn zwei
Elemente
Teilmenge eines Ordnungsintervalls ist, d.h., wenn zwei
Elemente ![]() existieren, so daß
existieren, so daß ![]() oder, was äquivalent dazu ist,
oder, was äquivalent dazu ist, ![]() gilt.
Eine von oben beschränkte bzw. von unten beschränkte Menge ist eine Menge,
für die eine obere bzw. eine untere Schranke in
gilt.
Eine von oben beschränkte bzw. von unten beschränkte Menge ist eine Menge,
für die eine obere bzw. eine untere Schranke in ![]() existiert.
existiert.