|
|
|
|
eine gegebene Distribution, dann heißt die Distribution 
,
definiert durch
von 
.
Seien 
eine stetig differenzierbare Funktion, etwa auf 
(damit ist
lokalsummierbar auf
und
als Distribution auffaßbar), 
ihre klassische
Ableitung und 
ihre distributionelle Ableitung der Ordnung 
.
Dann gilt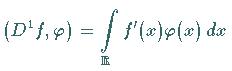 
,
woraus durch partielle Integration
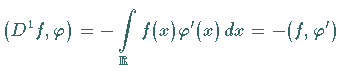folgt.
Im Falle einer regulären Distribution
erhält man wegen
die verallgemeinerte Ableitung der Funktion
im Sinne von SOBOLEW.
| Beispiel A | |
-Distribution.
| Beispiel B | |
|
Bei der mathematischen Modellierung von technischen und physikalischen Problemen treten
häufig (in gewisser Hinsicht idealisierte) auf einen Punkt konzentrierte Einwirkungen,
wie ,,punktförmige`` Kräfte, Nadelimpulse, Stoßvorgänge usw. auf,
die mathematisch ihren Ausdruck in der Verwendung der
Die Bewegungsgleichung eines Feder-Masse-Systems, auf das zum Zeitpunkt | |
|
|
als Massendichte
für eine im Punkt 
eines Balkens der Länge 
konzentrierte Punktmasse 
.
eine
momentane äußere Kraft der Größe 
einwirkt, hat die Form
.
Mit den Anfangsbedingungen 
ist
die Lösung.