Für ein beliebiges (offenes) Gebiet  bezeichnet
bezeichnet
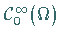 die Menge aller in
die Menge aller in 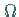 beliebig oft differenzierbaren
Funktionen
beliebig oft differenzierbaren
Funktionen 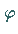 mit kompaktem Träger, d.h. die Menge
ist kompakt in
mit kompaktem Träger, d.h. die Menge
ist kompakt in 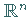 und liegt in
und liegt in 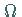 ,
während mit
,
während mit 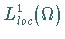 die
Menge aller bezüglich des LEBESGUE-Maßes im
die
Menge aller bezüglich des LEBESGUE-Maßes im 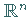 lokalsummierbaren Funktionen, d.h. aller (Klassen von äquivalenten) auf
lokalsummierbaren Funktionen, d.h. aller (Klassen von äquivalenten) auf
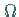 meßbaren Funktionen
meßbaren Funktionen  mit
mit
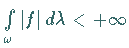 für jedes beschränkte Gebiet
für jedes beschränkte Gebiet
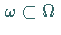 ,
bezeichnet wird.
Die beiden Mengen sind (mit den natürlichen algebraischen Operationen) Vektorräume.
Es gilt
,
bezeichnet wird.
Die beiden Mengen sind (mit den natürlichen algebraischen Operationen) Vektorräume.
Es gilt 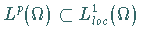 für
für 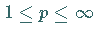 und
für beschränktes
und
für beschränktes 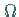 auch
auch 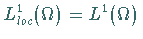 .
.
Faßt man die Elemente aus 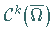 als die von ihnen in
als die von ihnen in
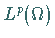 erzeugten Klassen auf, so gilt bei beschränktem
erzeugten Klassen auf, so gilt bei beschränktem 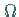 die Inklusion
die Inklusion
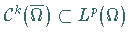 ,
wobei
,
wobei
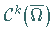 sogar dicht liegt.
Ist
sogar dicht liegt.
Ist 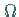 unbeschränkt, so liegt (in diesem Sinn) die Menge
unbeschränkt, so liegt (in diesem Sinn) die Menge
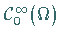 dicht in
dicht in 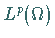 .
.
Die Formel der partiellen Integration hat für eine vorgegebene feste Funktion
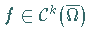 und eine beliebige Funktion
und eine beliebige Funktion
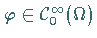 wegen
wegen
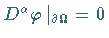 die Gestalt
die Gestalt
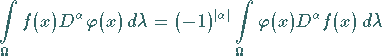 |
(12.207) |
für 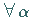 mit
mit 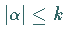 ,
die man als Ausgangspunkt für den
Begriff der verallgemeinerten Ableitung einer Funktion
,
die man als Ausgangspunkt für den
Begriff der verallgemeinerten Ableitung einer Funktion 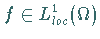 nehmen
kann.
nehmen
kann.
![]() als die von ihnen in
als die von ihnen in
![]() erzeugten Klassen auf, so gilt bei beschränktem
erzeugten Klassen auf, so gilt bei beschränktem ![]() die Inklusion
die Inklusion
![]() ,
wobei
,
wobei
![]() sogar dicht liegt.
Ist
sogar dicht liegt.
Ist ![]() unbeschränkt, so liegt (in diesem Sinn) die Menge
unbeschränkt, so liegt (in diesem Sinn) die Menge
![]() dicht in
dicht in ![]() .
.
![]() und eine beliebige Funktion
und eine beliebige Funktion
![]() wegen
wegen
![]() die Gestalt
die Gestalt