Konvexe Mengen
Eine Teilmenge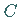 
eines reellen Vektorraumes 
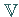heißt konvex , wenn für
jedes Paar von Vektoren 
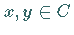alle Vektoren der Form
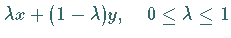ebenfalls zu
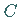gehören.
Mit anderen Worten, die Menge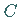
ist konvex, wenn sie mit je zwei Elementen die gesamte
Verbindungsstrecke
 |
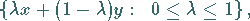(12.15) |
auch Intervall genannt, zwischen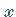 
und 
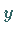enthält.
Beispiele konvexer Mengen in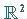 
sind die mit 
und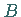 
bezeichneten Mengen in der
folgenden Abbildung.
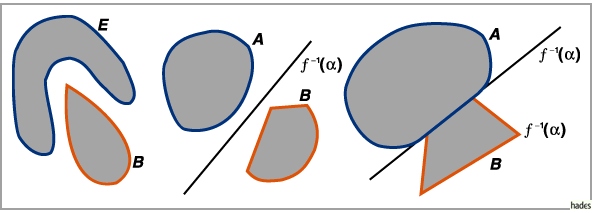
Siehe dazu auch Abschnitt Trennung konvexer Mengen.
Der Durchschnitt beliebig vieler konvexer Mengen ist wieder eine konvexe Menge, wobei
vereinbarungsgemäß die leere Menge als konvex angesehen wird.
Demzufolge existiert zu jeder Teilmenge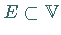 
eine kleinste konvexe Menge, die
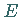enthält, nämlich der Durchschnitt aller konvexen und
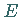enthaltenden Teilmengen
von .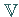
Sie heißt konvexe Hülle der Menge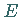
und wird mit 
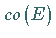bezeichnet.
Die konvexe Hülle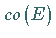
ist mit der Menge aller konvexen Linearkombinationen
von Elementen aus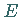
identisch, d.h.,
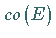besteht aus allen Elementen der Form
,
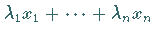wobei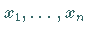 
beliebige
Elemente aus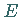
sind und 
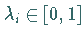der Gleichung
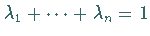genügen.
Lineare und affine Teilräume sind stets konvex.
