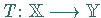|
|
|
|
des normierten Raums
in den normierten Raum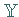 
heißt kompakt , wenn das Bild 
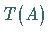jeder
beschränkten Menge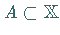 
eine relativkompakte Menge in
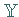ist.
Ist der Operator 
zudem noch stetig, dann heißt er vollstetig .
Jeder kompakte lineare Operator ist beschränkt und demzufolge vollstetig.
Für die Kompaktheit eines linearen Operators genügt es zu fordern, daß er die
Einheitskugel aus
in eine relativkompakte Menge in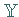
überführt.
|
|