Trennung konvexer Mengen
Man nennt zwei Teilmengen 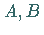 eines reellen normierten Raumes
eines reellen normierten Raumes  durch eine
Hyperebene trennbar , wenn ein Funktional
durch eine
Hyperebene trennbar , wenn ein Funktional 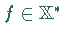 existiert, so daß gilt:
existiert, so daß gilt:
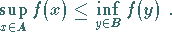 |
(12.170) |
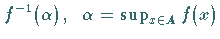 ist die trennende Hyperebene,
was nichts anderes besagt, als daß die Mengen in den verschiedenen Halbräumen
ist die trennende Hyperebene,
was nichts anderes besagt, als daß die Mengen in den verschiedenen Halbräumen
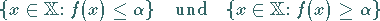 |
(12.171) |
liegen. In den folgenden zwei Abbildungen sind zwei Fälle der Trennung durch eine
Hyperebene dargestellt.
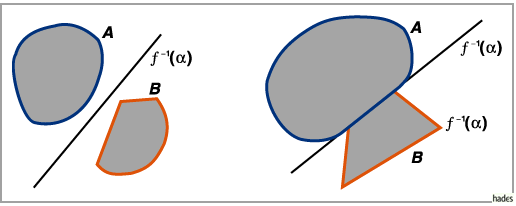
Entscheidend für die Trennung zweier Mengen ist weniger ihre Disjunktheit.
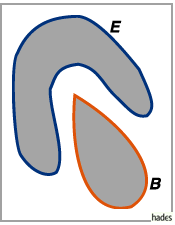
In der nächsten Abbildung sind zwei Mengen 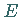 und
und 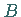 dargestellt, die nicht trennbar
sind, obwohl
dargestellt, die nicht trennbar
sind, obwohl 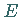 und
und 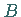 disjunkt sind und
disjunkt sind und 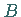 konvex.
Vielmehr ist die Konvexität der Mengen von Bedeutung, da nicht ausgeschlossen ist,
daß beide zu trennenden Mengen gemeinsame Punkte besitzen, durch die die Hyperebene
verläuft.
konvex.
Vielmehr ist die Konvexität der Mengen von Bedeutung, da nicht ausgeschlossen ist,
daß beide zu trennenden Mengen gemeinsame Punkte besitzen, durch die die Hyperebene
verläuft.
Es gilt:
Ist  eine konvexe Menge eines normierten Raumes
eine konvexe Menge eines normierten Raumes  mit nichtleerem Inneren
mit nichtleerem Inneren 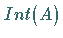 und
und 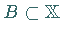 eine nichtleere konvexe Menge mit
eine nichtleere konvexe Menge mit 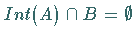 ,
dann
sind
,
dann
sind  und
und 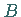 trennbar.
Ein (reelles lineares) Funktional
trennbar.
Ein (reelles lineares) Funktional 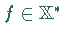 heißt Stützfunktional
an die Menge
heißt Stützfunktional
an die Menge  im Punkt
im Punkt 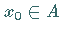 ,
wenn es eine solche Zahl
,
wenn es eine solche Zahl 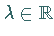 gibt, für die
gibt, für die 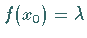 und
und 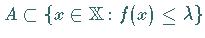 gilt.
gilt.
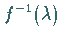 heißt dann Stützhyperebene im Punkt
heißt dann Stützhyperebene im Punkt 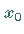 an
an 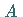 .
Für eine konvexe Menge
.
Für eine konvexe Menge 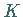 mit nichtleerem Inneren existiert in jedem ihrer Randpunkte
ein Stützfunktional.
mit nichtleerem Inneren existiert in jedem ihrer Randpunkte
ein Stützfunktional.
Auf der Trennbarkeit konvexer Mengen beruht der Beweis der
KUHN-TUCKER-Bedingungen, aus denen sich praktische Verfahren zur
Bestimmung des Minimums eines konvexen Optimierungsproblems herleiten lassen
(s. Lit. 12.5).