Gegeben ist die Integralgleichung
 |
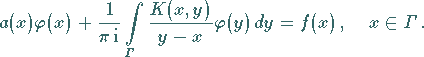(11.78) |
Hier ist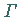 
ein System endlich vieler glatter, doppelpunktfreier, geschlossener
Kurven in der komplexen Ebene, die ein zusammenhängendes Innengebiet 
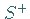mit
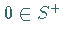und ein Außengebiet 
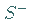bilden.
Dabei liegt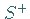
beim Durchlauf zur Linken von 
.
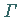Für die Betrachtung von Kurvensystemen, bestehend aus stückweise glatten, offenen
oder geschlossenen Kurven (s. Lit. 11.2).
Eine Funktion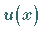 
ist auf
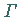HÖLDER-stetig, falls für
beliebige Paare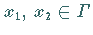 
gilt:
 |
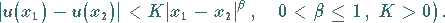(11.79) |
Die Funktionen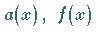 
und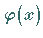 
werden als HÖLDER-stetig mit
dem Exponenten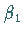 
und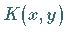 
bezüglich beider Argumente HÖLDER-stetig
mit dem Exponenten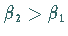 
angenommen.
Der Kern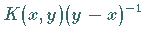 
hat für 
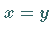eine starke Singularität.
Das Integral existiert aber als CAUCHYscher Hauptwert.
Mit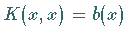 
und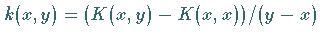 
ergibt sich (11.78) in
der Form
 |
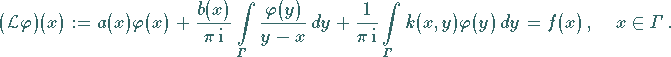(11.80a) |
Der Ausdruck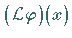 
beschreibt in verkürzter Form die linke Seite der
Integralgleichung.
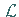ist ein singulärer Operator.
Die Kernfunktion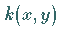 
ist nur schwach singulär.
Es gelte zusätzlich die Normalitätsbedingung
.
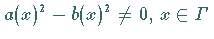Die Gleichung
 |
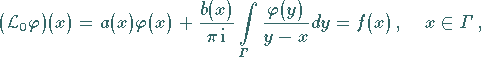(11.80b) |
ist die zu (11.80a) zugeordnete charakteristische Gleichung .
Der Operator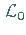 
ist der charakteristische Teil des Operators 
.
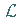Die zu (11.80a) transponierte Integralgleichung lautet:
