|
|
|
|
das Integral zu beseitigen bzw.
geeignet zu substituieren.
Wird die Stetigkeit von 
und 
sowie im Fall einer
Integralgleichung 2. Art die Differenzierbarkeit von
vorausgesetzt, so ergibt
die Differentiation von
:
| Beispiel | |||
|
Gesucht ist eine Funktion Zweimaliges Ableiten nach
liefert
Das in der letzten Zeile auftretende Integral entspricht der linken Seite der Integralgleichung (11.62). Das ergibt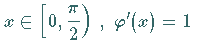 
und, da
für  ,
also  .
Zur Bestimmung der Konstanten 
setzt man in (11.63a)  .
Somit ist  ,
und die Lösung von (11.62) lautet:  .
| |||
Hinweis: Ist der Kern einer VOLTERRAschen Integralgleichung ein Polynom, so
gelingt es mit der Methode der Differentiation immer, die Integralgleichung in eine
lineare Differentialgleichung zu überführen.
Ist dabei 
der Grad der höchsten im Kern auftretenden -Potenz, so erhält man
durch 
-maliges Differenzieren nach
eine Differentialgleichung der Ordnung
im Falle einer Integralgleichung 1. Art bzw. der Ordnung 
für eine
Integralgleichung 2. Art.
Dabei wird vorausgesetzt, daß sowohl
als auch 
entsprechend oft
differenzierbar sind.
| Beispiel | |||||
|
Dreimaliges Differenzieren nach
ergibt
Die allgemeine Lösung dieser Differentialgleichung lautet:
Setzt man in (11.65a) bzw. (11.65b) 
ein, so erhält man
und somit  .
Die Lösung der Integralgleichung (11.64) ist also  .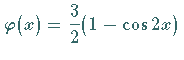
| |||||
|
|
als
Lösung von
