Orthonormalsystem
Zwei quadratisch integrierbare Funktionen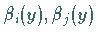 
mit 
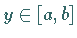werden als orthogonal bezeichnet, falls für 
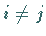gilt
 |
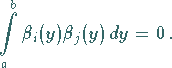(11.44a) |
Ein Funktionensystem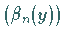 
im Raum 
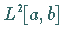wird als Orthonormalsystem
bezeichnet, wenn die Beziehungen
 |
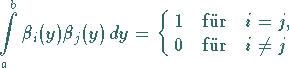(11.44b) |
erfüllt sind.
Ein Orthonormalsystem ist überdies vollständig , wenn in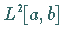
keine
Funktion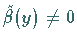 
existiert, die zu allen Funktionen dieses
Orthonormalsystems orthogonal ist.
Ein vollständiges Orthonormalsystem besteht aus abzählbar vielen Funktionen, die eine
Basis des Raumes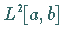
bilden.
Um aus einem Funktionensystem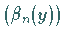
ein Orthonormalsystem 
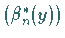zu
ermitteln, kann das
GRAM-SCHMIDTsche Orthogonalisierungsverfahren
verwendet werden.
Es bestimmt sukzessive für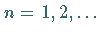 
die Koeffizienten
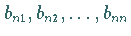derart, daß
 |
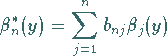(11.44c) |
normiert und zu allen Funktionen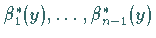 
orthogonal ist.
