Die Koeffizientenmatrix ist regulär, wenn die
lineare Unabhängigkeit der Funktionen
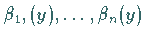vorausgesetzt wird.
Die so ermittelte Lösung (11.39a) ist jedoch nicht die einzige Lösung der
Integralgleichung.
Im Gegensatz zur
FREDHOLMschen Integralgleichung 2. Art mit ausgeartetem Kern
ist die homogene Integralgleichung immer lösbar. Ist
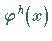eine solche Lösung der homogenen Gleichung und 
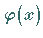eine Lösung
von (11.38a), dann ist auch 
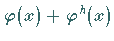eine Lösung von
(11.38a).
Um alle Lösungen der homogenen Gleichung zu bestimmen, wird die Gleichung
(11.38c) mit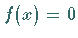 
betrachtet.
Werden die Funktionen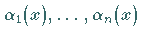 
als linear unabhängig
vorausgesetzt, dann ist die Gleichung genau dann erfüllt, wenn gilt
 |
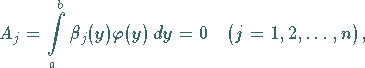(11.40) |
d.h., jede zu allen Funktionen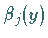 
orthogonale Funktion 
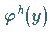löst
die homogene Integralgleichung.
