Tensorprodukt-Approximation
Eine häufig verwendete Näherung für den Kern ist die
Tensorprodukt-Approximation der Form
 |
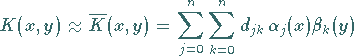(11.31a) |
mit linear unabhängigen Funktionen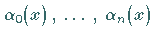 
bzw.
.
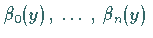Diese Funktionen werden vorgegeben, und die Koeffizienten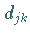 
können so bestimmt
werden, daß die Doppelsumme den Kern in einem gewissen Sinne gut approximiert.
Umformung von (11.31a) mit ausgeartetem Kern ergibt:
 |
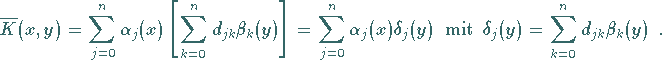(11.31b) |
Somit kann das unter
Integralgleichungen mit ausgearteten Kernen vorgestellte
Verfahren zur Lösung der Integralgleichung
 |
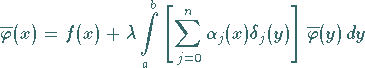(11.31c) |
zur Anwendung kommen.
Bei der Auswahl der Funktionen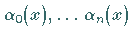 
bzw.
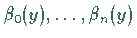sollte beachtet werden, daß die Zahlen
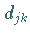in
(11.31a) einfach zu bestimmen sind und der Rechenaufwand zur Behandlung von
(11.31c) gering bleibt.
