Spezieller Spline-Ansatz
Für eine spezielle Kernapproximation auf dem Integrationsintervall 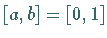 wird
wird
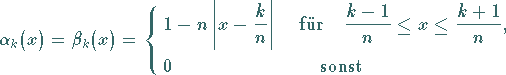 |
(11.32) |
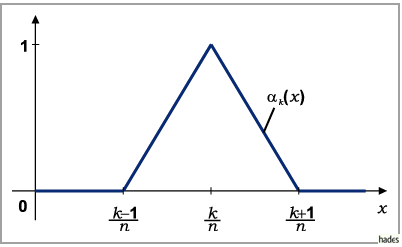
gewählt. Die Funktion 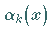 ist nur in dem Intervall
ist nur in dem Intervall
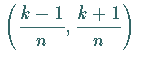 ,
dem sogenannten Träger ,
ungleich Null (s. Abbildung).
,
dem sogenannten Träger ,
ungleich Null (s. Abbildung).
Zur Bestimmung der Koeffizienten 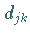 in (11.31a) betrachte man
in (11.31a) betrachte man
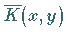 an den Stellen
an den Stellen 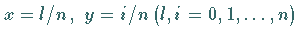 .
Dann gilt
.
Dann gilt
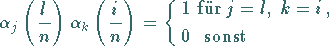 |
(11.33) |
und folglich 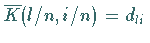 .
Aus diesem Grund setzt man
.
Aus diesem Grund setzt man
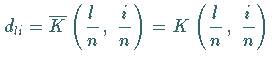 .
Die Gleichung (11.31a) hat damit die Form
.
Die Gleichung (11.31a) hat damit die Form
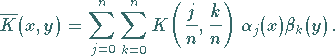 |
(11.34) |
Die Lösung von (11.31c) hat bekanntlich die Darstellung
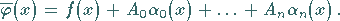 |
(11.35) |
Der Ausdruck  ist dabei ein Polygonzug, der an
der Stelle
ist dabei ein Polygonzug, der an
der Stelle 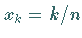 den Wert
den Wert 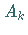 annimmt.
Bei der Lösung von (11.31c) nach dem Verfahren für ausgeartete Kerne ergibt
sich ein lineares Gleichungssystem für die Zahlen
annimmt.
Bei der Lösung von (11.31c) nach dem Verfahren für ausgeartete Kerne ergibt
sich ein lineares Gleichungssystem für die Zahlen 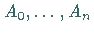 :
:
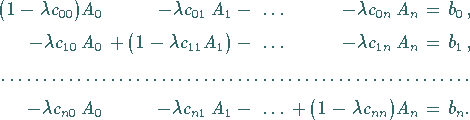 |
(11.36a) |
Dabei ist
Für die Integrale ergibt sich
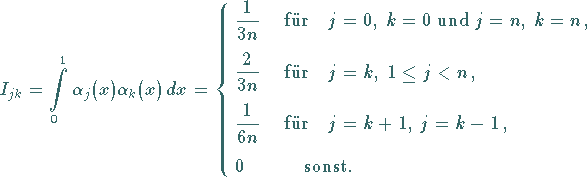 |
(11.36c) |
Die Zahlen 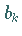 in (11.36a) sind festgelegt durch
in (11.36a) sind festgelegt durch
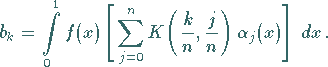 |
(11.36d) |
Werden die Zahlen 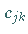 aus (11.36a) zur Matrix
aus (11.36a) zur Matrix 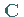 ,
die Werte
,
die Werte
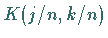 zur Matrix
zur Matrix 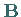 und die Werte
und die Werte 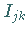 zur Matrix
zur Matrix 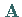 zusammengefaßt, und wird aus den Zahlen
zusammengefaßt, und wird aus den Zahlen 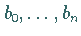 der Vektor
der Vektor
 und aus den gesuchten Zahlen
und aus den gesuchten Zahlen 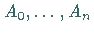 der Vektor
der Vektor
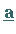 gebildet, dann hat das Gleichungsystem (11.36a) in
Matrizenschreibweise die Form
gebildet, dann hat das Gleichungsystem (11.36a) in
Matrizenschreibweise die Form
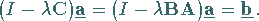 |
(11.36e) |
Falls die Matrix 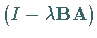 regulär ist, hat dieses System eine eindeutige
Lösung
regulär ist, hat dieses System eine eindeutige
Lösung 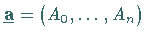 .
.
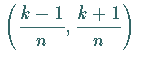 ,
dem sogenannten Träger ,
ungleich Null (s. Abbildung).
,
dem sogenannten Träger ,
ungleich Null (s. Abbildung).
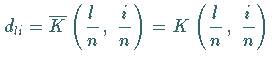 .
Die Gleichung (11.31a) hat damit die Form
.
Die Gleichung (11.31a) hat damit die Form