Semidiskretes Problem
Zur Bearbeitung der Integralgleichung (11.23) wird das Integral durch einen
Näherungsausdruck ersetzt.
Derartige Näherungen bezeichnet man als Quadraturformeln .
Sie haben die Form
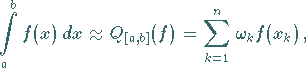 |
(11.24) |
d.h., anstelle des Integrals steht eine Summe mit Zahlen 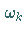 gewichteter
Funktionswerte an den Stützstellen
gewichteter
Funktionswerte an den Stützstellen 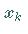 .
Die
.
Die 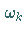 sind dabei (unabhängig von
sind dabei (unabhängig von 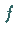 )
geeignet gewählt.
Damit kann (11.23) näherungsweise geschrieben werden:
)
geeignet gewählt.
Damit kann (11.23) näherungsweise geschrieben werden:
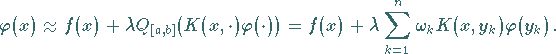 |
(11.25a) |
Die Quadraturformel 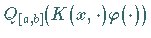 hängt dabei noch von der
Variablen
hängt dabei noch von der
Variablen 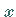 ab.
Der Punkt im Argument der Funktion deutet an, daß die Quadraturformel bezüglich der
unabhängigen Variablen
ab.
Der Punkt im Argument der Funktion deutet an, daß die Quadraturformel bezüglich der
unabhängigen Variablen 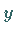 angewendet worden ist.
Man geht über zur Gleichung
angewendet worden ist.
Man geht über zur Gleichung
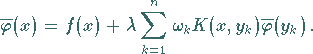 |
(11.25b) |
Die Funktion 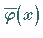 bildet eine Approximation für die exakte Lösung
bildet eine Approximation für die exakte Lösung
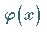 .
Man bezeichnet (11.25b) als ein semidiskretes Problem , da bezüglich der
Variablen
.
Man bezeichnet (11.25b) als ein semidiskretes Problem , da bezüglich der
Variablen 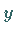 zu diskreten Werten übergegangen wurde, während die Variable
zu diskreten Werten übergegangen wurde, während die Variable 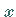 noch
beliebig wählbar ist.
noch
beliebig wählbar ist.
Wenn für eine Funktion 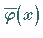 die Gleichung (11.25b) für
alle
die Gleichung (11.25b) für
alle 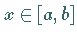 gilt, ist diese natürlich auch an den Stützstellen
gilt, ist diese natürlich auch an den Stützstellen 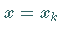 erfüllt:
erfüllt:
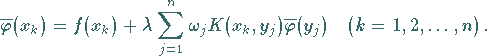 |
(11.25c) |
Dies ist ein lineares Gleichungssystem, bestehend aus 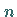 Gleichungen für die
Gleichungen für die 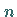 Unbekannten
Unbekannten 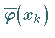 .
Durch Einsetzen dieser Lösungswerte in (11.25b) ist die Lösung des
semidiskreten Problems gegeben.
Die Genauigkeit und der Rechenaufwand dieses Verfahrens hängen von der Güte der
Quadraturformel ab.
Benutzt man z.B. die linksseitige Rechteckformel mit äquidistanten
Stützstellen
.
Durch Einsetzen dieser Lösungswerte in (11.25b) ist die Lösung des
semidiskreten Problems gegeben.
Die Genauigkeit und der Rechenaufwand dieses Verfahrens hängen von der Güte der
Quadraturformel ab.
Benutzt man z.B. die linksseitige Rechteckformel mit äquidistanten
Stützstellen
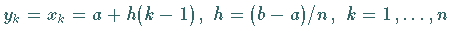 :
:
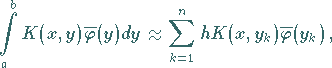 |
(11.26a) |
so erhält das System (11.25c) unter Verwendung der Bezeichnungen
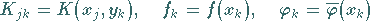 |
(11.26b) |
die Form:
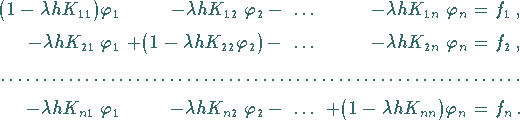 |
(11.26c) |
Genau dieses System wurde schon bei der Untersuchung der
FREDHOLMschen Lösungsmethode hergeleitet.
Da die linksseitige Rechteckformel aber nicht sehr genau ist,
müssen für eine gute Approximation des Integrals eine große Anzahl von
Stützstellen einbezogen werden, wodurch die Dimension des Gleichungssystems wächst.
Es empfiehlt sich daher, geeignetere Quadraturformeln heranzuziehen.
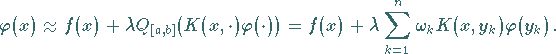
![]() hängt dabei noch von der
Variablen
hängt dabei noch von der
Variablen ![]() ab.
Der Punkt im Argument der Funktion deutet an, daß die Quadraturformel bezüglich der
unabhängigen Variablen
ab.
Der Punkt im Argument der Funktion deutet an, daß die Quadraturformel bezüglich der
unabhängigen Variablen ![]() angewendet worden ist.
Man geht über zur Gleichung
angewendet worden ist.
Man geht über zur Gleichung
![]() die Gleichung (11.25b) für
alle
die Gleichung (11.25b) für
alle ![]() gilt, ist diese natürlich auch an den Stützstellen
gilt, ist diese natürlich auch an den Stützstellen ![]() erfüllt:
erfüllt: