Isoperimetrisches Problem
Das allgemeine isoperimetrische Problem besteht darin, unter allen ebenen
Flächenstücken mit vorgegebenem Umfang das flächengrößte zu bestimmen.
Die Lösung dieses Problems (ein Kreis mit dem vorgegebenen Umfang) soll auf die
Königin DIDO zurückgehen, die der Sage nach bei der Gründung Karthagos nur
soviel Land nehmen durfte, wie sie mit einer Stierhaut umschließen konnte.
Sie schnitt die Haut in feine Streifen und legte sie zu einem Kreis zusammen.
Ein Spezialfall des allgemeinen isoperimetrischen Problems besteht in der Aufgabe, in
einem kartesischen Koordinatensystem eine Verbindungskurve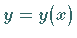 
der Punkte 
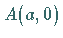und 
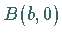zu finden, die eine vorgegebene Länge 
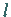hat und mit der
Verbindungsstrecke 
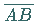die größte Fläche umschließt
(s. Abbildung).
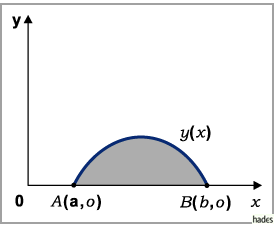
Die mathematische Formulierung lautet:
Man bestimme eine einmal stetig differenzierbare Funktion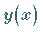 
,
für die
 |
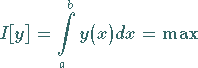(10.8a) |
gilt und die die Nebenbedingung
 |
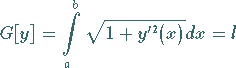(10.8b) |
sowie die Randbedingungen
 |
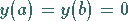(10.8c) |
erfüllt.
