Division
Die Division zweier komplexer Zahlen wird als die zur Multiplikation inverse Operation
definiert. In algebraischer Schreibweise ergibt sich
 |
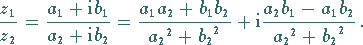(1.140a) |
Die trigonometrische Schreibweise lautet
 |
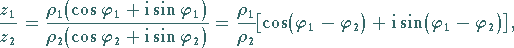(1.140b) |
d.h., der Betrag des Quotienten ist gleich dem Quotienten aus den Beträgen des
Dividenden und des Divisors, während das Argument des Quotienten gleich der Differenz
der beiden Argumente ist.
In der Exponentialform erhält man
 |
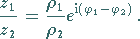(1.140c) |
In der geometrischen Definition ergibt sich der Vektor, der den Quotienten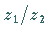 
darstellt, durch Drehung des die Zahl 
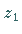darstellenden Vektors um den Winkel
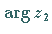im Uhrzeigersinn sowie durch Kontraktion dieses Vektors mit dem Faktor
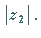
Hinweis: Eine Division durch Null ist nicht möglich.
