Multiplikation
Die Multiplikation zweier komplexer Zahlen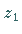 
und 
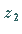in der algebraischen Schreibweise
ist definiert durch die Formel
 |
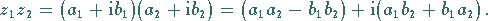(1.139a) |
In der trigonometrischen Schreibweise gilt
 |
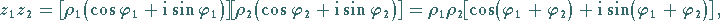(1.139b) |
d.h., der Betrag des Produkts ist gleich dem Produkt der Beträge der Faktoren,
während das Argument des Produkts gleich der Summe der Argumente der Faktoren ist.
In der Exponentialform erhält man
 |
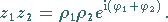(1.139c) |
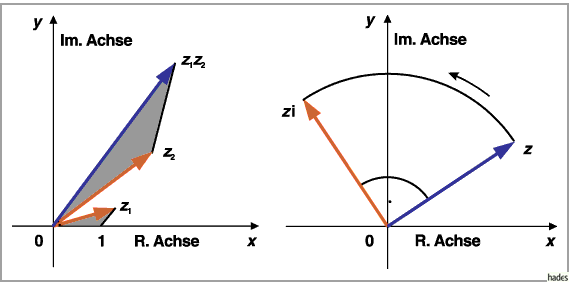
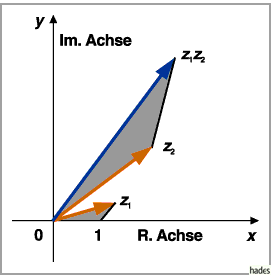
In der geometrischen Interpretation wird der Produktvektor, der das Produkt von
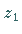und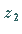
darstellt, durch Drehung des Vektors
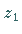im entgegengesetzten
Uhrzeigersinn um den Winkel, der dem Argument von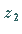
entspricht, gedreht und
durch Multiplikation dieses Vektors mit dem Faktor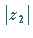 
gestreckt.
Das Produkt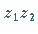 
kann auch durch Konstruktion eines ähnlichen Dreiecks gewonnen
werden.
Dabei ist zu berücksichtigen, daß die Multiplikation einer komplexen Zahl
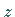mit i eine Drehung ihres Vektors um den Winkel 
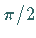bedeutet, während
der Modul konstant bleibt.
