Trigonometrische Form der komplexen Zahlen
Die Darstellung
 |
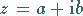(1.134a) |
einer komplexen Zahl wird algebraische Form genannt.
Wenn Polarkoordinaten anstelle der kartesischen Koordinaten verwendet werden,
dann ergibt sich die trigonometrische Form der komplexen Zahl
 |
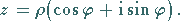(1.134b) |
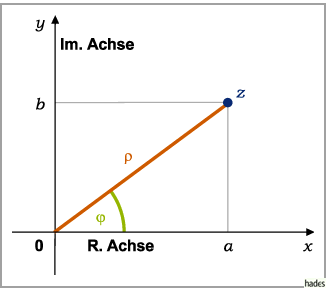
Man bezeichnet
 |
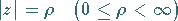(1.134c) |
als Absolutbetrag oder Modul und
 |
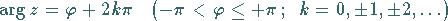(1.134d) |
als Argument der komplexen Zahl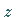 
.
Der Winkel 
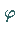heißt Hauptwert des Argumentes der komplexen Zahl
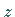(1.134b).
Der Zusammenhang zwischen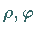 
und 
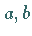für einen Punkt ist derselbe
wie der zwischen den kartesischen Koordinaten und den Polarkoordinaten dieses Punktes
(s. Übergang zwischen kartesischen und Polarkoordinaten):
 |
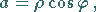(1.135a) |
 |
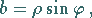(1.135b) |
 |
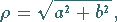(1.135c) |
bzw.
Die komplexe Zahl 
hat den Modul Null, während das Argument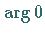 
unbestimmt
ist.
