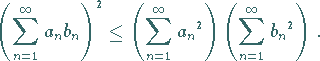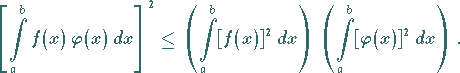1. Cauchy-Schwarzsche Ungleichung für reelle Zahlen
Die CAUCHY-SCHWARZsche Ungleichung gilt für alle reellen Zahlen
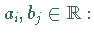
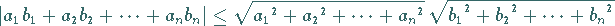 |
(1.117a) |
oder
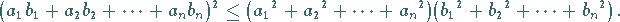 |
(1.117b) |
Für zwei endliche Zahlenfolgen mit jeweils 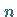 Zahlen ist der Betrag der Summe
ihrer paarweisen Produkte kleiner oder gleich dem Produkt der beiden Quadratwurzeln
aus den Summen der Quadrate dieser Zahlen.
Das Gleichheitszeichen gilt nur für
Zahlen ist der Betrag der Summe
ihrer paarweisen Produkte kleiner oder gleich dem Produkt der beiden Quadratwurzeln
aus den Summen der Quadrate dieser Zahlen.
Das Gleichheitszeichen gilt nur für 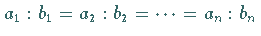 .
.
Wenn  ist und
ist und 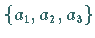 und
und 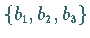 als
rechtwinklige kartesische Koordinaten von Vektoren aufgefaßt werden, dann
besagt die Ungleichung von CAUCHY-SCHWARZ, daß das skalare Produkt
zweier Vektoren betragsmäßig kleiner oder gleich dem Produkt der Beträge
dieser Vektoren ist.
Wenn
als
rechtwinklige kartesische Koordinaten von Vektoren aufgefaßt werden, dann
besagt die Ungleichung von CAUCHY-SCHWARZ, daß das skalare Produkt
zweier Vektoren betragsmäßig kleiner oder gleich dem Produkt der Beträge
dieser Vektoren ist.
Wenn 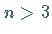 ist, dann kann diese Aussage auf Vektoren im
ist, dann kann diese Aussage auf Vektoren im 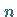 -dimensionalen
euklidischen Raum ausgedehnt werden.
-dimensionalen
euklidischen Raum ausgedehnt werden.
2. Cauchy-Schwarzsche Ungleichung für komplexe Zahlen
Für beliebige komplexe Zahlen 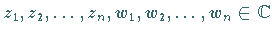 gilt:
gilt:
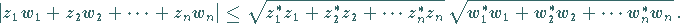 |
(1.118) |
Mit 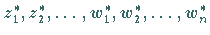 werden die
konjugiert komplexen Zahlen zu
werden die
konjugiert komplexen Zahlen zu
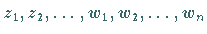 bezeichnet.
bezeichnet.
3. Cauchy-Schwarzsche Ungleichung für konvergente unendliche Reihen und
Integrale
Ein Analogon zu (1.117b) ist die CAUCHY-SCHWARZsche Ungleichung für
konvergente unendliche Reihen sowie für bestimmte Integrale:
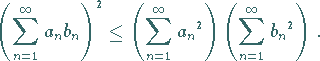 |
(1.119) |
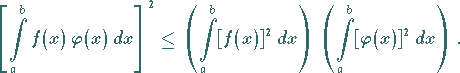 |
(1.120) |