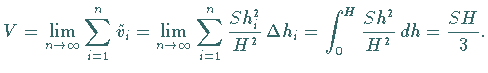|
Berechnung des Rauminhalts einer Pyramide der Grundfläche  und der Höhe
und der Höhe 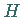 (s. linke Abbildung):
(s. linke Abbildung):
a) Zerlegung des zu berechnenden Rauminhaltes 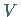 durch ebene Schnitte in
Volumina dünner Pyramidenstümpfe (s. mittlere Abbildung):
durch ebene Schnitte in
Volumina dünner Pyramidenstümpfe (s. mittlere Abbildung):
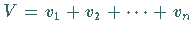 . .
b) Ersetzen eines jeden Pyramidenstumpfes durch ein Prisma 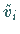 mit
der gleichen Höhe und einer Grundfläche, die gleich der oberen Grundfläche des
Pyramidenstumpfes ist (s. mittlere Abbildung).
Die Volumenabweichung ist eine infinitesimale Größe von höherer Ordnung als
mit
der gleichen Höhe und einer Grundfläche, die gleich der oberen Grundfläche des
Pyramidenstumpfes ist (s. mittlere Abbildung).
Die Volumenabweichung ist eine infinitesimale Größe von höherer Ordnung als
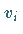 . .
c) Darstellung der Volumenformel 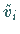 in der Form
in der Form
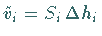 ,
wobei ,
wobei 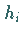 der Abstand der oberen Fläche von der
Pyramidenspitze ist.
Wegen
der Abstand der oberen Fläche von der
Pyramidenspitze ist.
Wegen 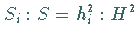 kann man schreiben:
kann man schreiben:
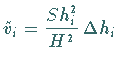 . .
d) Berechnung des Grenzwertes der Summe
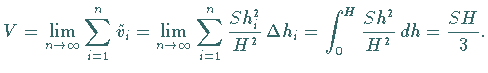
| 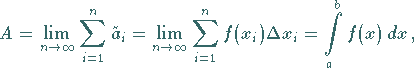
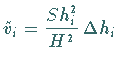 .
.