Graphische Integration
Graphische Integration ist eine graphische Verfahrensweise, um die als Kurve 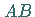 (s. Abbildung) gegebene Funktion
(s. Abbildung) gegebene Funktion 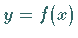 zu integrieren, d.h. das Integral
zu integrieren, d.h. das Integral
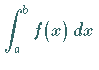 ,
das die Größe der Fläche
,
das die Größe der Fläche 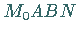 angibt, graphisch zu
berechnen.
angibt, graphisch zu
berechnen.
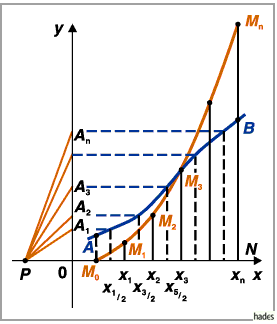
1. Das Intervall  wird durch die Punkte
wird durch die Punkte
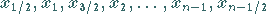 |
(8.55a) |
in 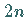 gleiche Teile eingeteilt, wobei das Ergebnis um so genauer ausfällt, je
größer die Anzahl der Teilungspunkte ist.
gleiche Teile eingeteilt, wobei das Ergebnis um so genauer ausfällt, je
größer die Anzahl der Teilungspunkte ist.
2. In den Teilungspunkten
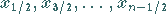 |
(8.55b) |
werden Lote bis zum Schnitt mit der Kurve errichtet.
Die so gewonnenen Ordinatenwerte werden als Strecken
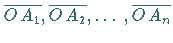 auf der
auf der 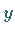 -Achse
abgetragen.
-Achse
abgetragen.
3. Auf der negativen 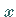 -Achse wird eine Strecke
-Achse wird eine Strecke 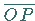 von
beliebiger Länge abgetragen, und der Punkt
von
beliebiger Länge abgetragen, und der Punkt 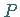 wird mit den Punkten
wird mit den Punkten
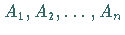 verbunden.
verbunden.
4. Durch den Punkt 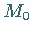 wird eine Parallele zu
wird eine Parallele zu 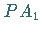 gezogen.
Diese schneidet die im Teilungspunkt
gezogen.
Diese schneidet die im Teilungspunkt 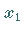 errichtete Senkrechte im Punkt
errichtete Senkrechte im Punkt 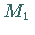 .
Durch den Punkt
.
Durch den Punkt 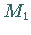 wird die Parallele zu
wird die Parallele zu 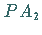 gezogen.
Diese schneidet die im Teilungspunt
gezogen.
Diese schneidet die im Teilungspunt 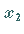 errichtete Senkrechte im Punkt
errichtete Senkrechte im Punkt 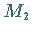 ,
usw. bis der Punkt
,
usw. bis der Punkt 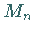 erreicht ist.
erreicht ist.
Zahlenmäßig ist das zu berechnende Integral gleich dem Produkt aus den Längen der
Strecken 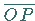 und
und 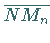 :
:
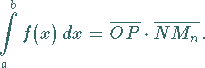 |
(8.56) |
Mit Hilfe der beliebig wählbaren Strecke 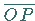 werden die Ausmaße der
Zeichnung bestimmt; je kleiner die zulässigen Abmessungen der Zeichnung sind, desto
größer ist
werden die Ausmaße der
Zeichnung bestimmt; je kleiner die zulässigen Abmessungen der Zeichnung sind, desto
größer ist 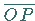 zu wählen.
Für
zu wählen.
Für 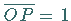 ergibt sich
ergibt sich 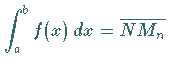 ,
und der
Polygonzug
,
und der
Polygonzug 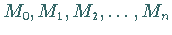 entspricht angenähert dem Kurvenbild der
Stammfunktion von
entspricht angenähert dem Kurvenbild der
Stammfunktion von 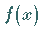 ,
d.h. dem unbestimmten Integral
,
d.h. dem unbestimmten Integral 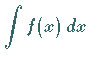 .
.
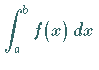 ,
das die Größe der Fläche
,
das die Größe der Fläche 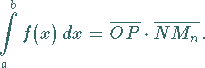
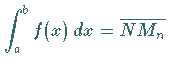 ,
und der
Polygonzug
,
und der
Polygonzug 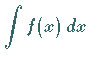 .
.