Integrale elementarer Funktionen
1. Grundintegrale:Die Grundintegrale können unmittelbar aus den Ableitungen bekannter elementarer
Funktionen gewonnen werden, da das unbestimmte Integrieren einer Funktion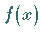 
das
Aufsuchen einer Stammfunktion 
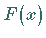bedeutet.
Die in der Tabelle Grundintegrale zusammengestellten Integrale ergeben
sich aus der Umkehrung der wichtigsten Differentiationsformeln der
Tabelle Ableitungen elementarer Funktionen.
Die Integrationskonstante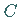 
ist weggelassen worden.
2. Allgemeiner Fall:
Bei der Lösung von Integralen wird versucht, ein gegebenes Integral durch algebraische
und trigonometrische Umformungen bzw. durch Anwendung von Integrationsregeln auf die
Grundintegrale zurückzuführen.
Die im Abschnitt Integrationsregeln angegebenen Integrationsmethoden
ermöglichen die Integration von Funktionen, die eine elementare Stammfunktion besitzen.
Die Integrationsergebnisse sind in der Tabelle Unbestimmte Integrale
zusammengestellt.
Folgende Hinweise sind bei der Benutzung zu beachten:
a) Die Integrationskonstante wurde meist weggelassen. Ausgenommen sind
einige Integrale, die in verschiedenen Formen mit verschiedenen beliebigen
Konstanten darstellbar sind.
b) Tritt in der Stammfunktion ein Ausdruck auf, der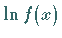 
enthält,
dann ist darunter stets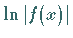 
zu verstehen.
c) Wenn die Stammfunktion durch eine Potenzreihe dargestellt ist, kann die Funktion
nicht elementar integriert werden.
Eine ausführlichere Zusammenstellung enthalten die Tabellenwerke dieser Taschenbuchserie
Lit. 8.1 und 8.3.
