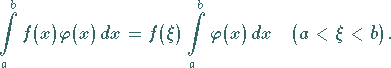Mittelwertsatz und verallgemeinerter Mittelwertsatz
1. Mittelwertsatz:
Wenn eine Funktion 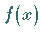 im Intervall
im Intervall 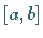 stetig ist, dann gibt es im Innern des
Intervalls mindestens einen Wert
stetig ist, dann gibt es im Innern des
Intervalls mindestens einen Wert 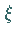 derart, daß für
derart, daß für 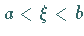 und für
und für
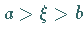 gilt:
gilt:
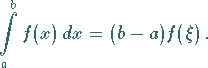 |
(8.47) |
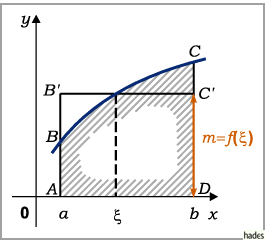
Der geometrische Sinn dieses Satzes besteht darin, daß es zwischen den Punkten 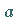 und
und 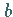 einen Punkt
einen Punkt 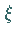 gibt, für den der Flächeninhalt der Figur
gibt, für den der Flächeninhalt der Figur 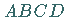 gleich dem
des Rechtecks
gleich dem
des Rechtecks 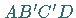 in der folgenden Abbildung ist.
in der folgenden Abbildung ist.
Der Wert
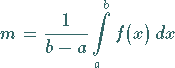 |
(8.48) |
heißt Mittelwert oder das arithmetische Mittel der
Funktion 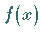 im Intervall
im Intervall 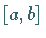 .
.
2. Verallgemeinerter Mittelwertsatz:
Sind die Funktionen 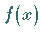 und
und 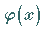 im abgeschlossenen Intervall
im abgeschlossenen Intervall 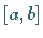 stetig
und ändert
stetig
und ändert 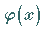 in diesem Intervall sein Vorzeichen nicht, dann gibt es im
Innern des Integrationsgebietes mindestens eine Zahl
in diesem Intervall sein Vorzeichen nicht, dann gibt es im
Innern des Integrationsgebietes mindestens eine Zahl 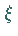 ,
so daß gilt:
,
so daß gilt:
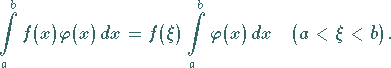 |
(8.49) |
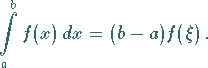
![]() und
und ![]() einen Punkt
einen Punkt ![]() gibt, für den der Flächeninhalt der Figur
gibt, für den der Flächeninhalt der Figur ![]() gleich dem
des Rechtecks
gleich dem
des Rechtecks ![]() in der folgenden Abbildung ist.
in der folgenden Abbildung ist.
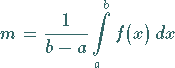
![]() im Intervall
im Intervall ![]() .
.
![]() und
und ![]() im abgeschlossenen Intervall
im abgeschlossenen Intervall ![]() stetig
und ändert
stetig
und ändert ![]() in diesem Intervall sein Vorzeichen nicht, dann gibt es im
Innern des Integrationsgebietes mindestens eine Zahl
in diesem Intervall sein Vorzeichen nicht, dann gibt es im
Innern des Integrationsgebietes mindestens eine Zahl ![]() ,
so daß gilt:
,
so daß gilt: