Stammfunktion oder Integral einer gegebenen Funktion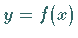 
,
die in einem
zusammenhängenden Intervall 
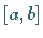definiert ist, wird eine differenzierbare Funktion
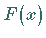genannt, die in demselben Intervall definiert ist und deren Ableitung gleich 
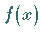ist:
 |
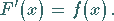(8.1) |
Da bei der Differentiation einer Funktion eine additiv auftretende Konstante verschwindet,
existieren zu einer gegebenen Funktion unendlich viele Stammfunktionen.
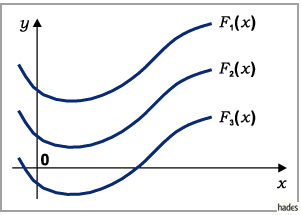
Die Differenz zweier Stammfunktionen ist eine Konstante.
Daher können die Bilder aller Stammfunktionen
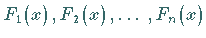zu einer gegebenen Funktion durch
Parallelverschiebung einer bestimmten Stammfunktion in Richtung der Ordinatenachse
erzeugt werden.
