Definition des Dreifachintegrals
Die Definition des Dreifachintegrals einer Funktion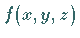 
von drei Variablen über
einen dreidimensionalen Bereich, z.B. den Raumteil 
,
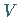erfolgt in Analogie zur
Definition des Doppelintegrals.
Man schreibt
 |
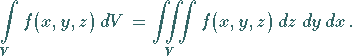(8.141) |
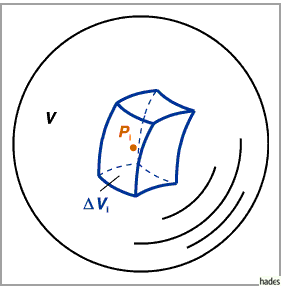
Das Volumen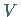 
wird in Elementarvolumina zerlegt, mit denen Produkte der
Art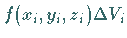 
gebildet werden, wobei der Punkt 
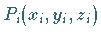im
Innern oder auf dem Rande eines Elementarvolumens liegen kann.
Das Dreifachintegral ist dann der Grenzwert der Summe derartiger Produkte für alle
Elementarvolumina, in die das Volumen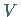
zerlegt wurde, und zwar für den Fall, daß
der Rauminhalt jedes Elementarvolumens gegen Null geht, d.h. ihre Anzahl gegen 
.
Dabei ist wie beim Doppelintegral zu beachten, daß der Durchmesser des
Elementarvolumens gegen Null strebt und nicht nur eine der möglichen Ausdehnungen.
Es gilt dann
 |
(8.142) |
