Konvergente und divergente Reihen
Man spricht von einer konvergenten Reihe (7.12), wenn die Folge
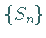der Partialsummen konvergiert.
Den Grenzwert
 |
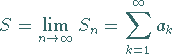(7.14) |
nennt man die Summe und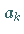 
das allgemeine Glied der Reihe.
Wenn der Grenzwert (7.14) nicht existiert, spricht man von einer
divergenten Reihe .
In diesem Falle können die Partialsummen unbegrenzt wachsen oder oszillieren.
Die Frage nach der Konvergenz einer unendlichen Reihe wird somit auf die Existenz eines
Grenzwertes der Folge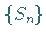 
zurückgeführt.
 |
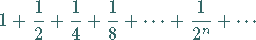(7.15) |
ist konvergent.
| Beispiel B |
|
Die harmonische Reihe
|
 |
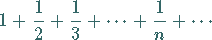(7.16) |
und die Reihen
 |
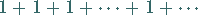(7.17) |
und
 |
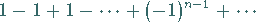(7.18) |
sind divergent.
Während für die Reihen (7.16) und (7.17)
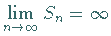ist, oszilliert (7.18).
