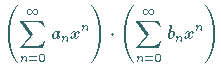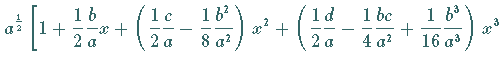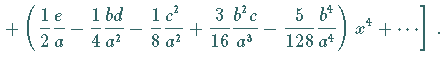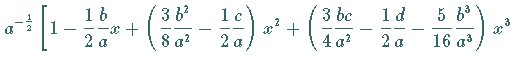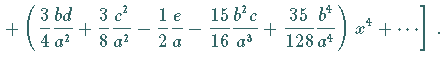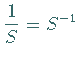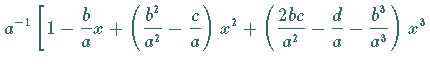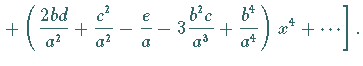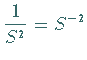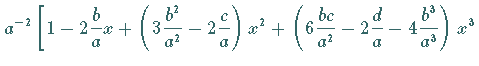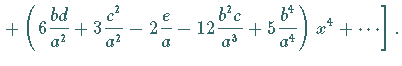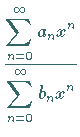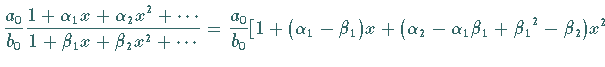1. Summe und Produkt von Potenzreihen
Konvergente Potenzreihen dürfen innerhalb ihres gemeinsamen Konvergenzbereiches
gliedweise addiert, miteinander multipliziert und mit einem beliebigen konstanten
Zahlenfaktor multipliziert werden.
Das Produkt zweier Potenzreihen ergibt sich zu
2. Erste Glieder einiger Potenzen von Potenzreihen
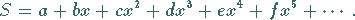 |
(7.80) |
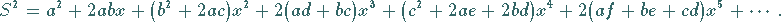 |
(7.81) |
3. Quotient zweier Potenzreihen
Diese Formel ergibt sich, indem der Quotient als Reihe mit unbestimmten Koeffizienten
angesetzt und mit der Nenner-Reihe ausmultipliziert wird, worauf die Koeffizienten der
entstehenden Reihe durch Koeffizientenvergleich mit der Zähler-Reihe bestimmt werden.
4. Umkehrung einer Potenzreihe
Ist die Reihe
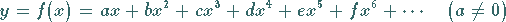 |
(7.87a) |
gegeben, dann versteht man unter ihrer Umkehrung die Reihe
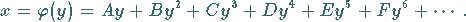 |
(7.87b) |
Die Koeffizienten ergeben sich zu
Die Konvergenz der Umkehrreihe muß in jedem Beispiel besonders untersucht werden.