Absolute Konvergenz und Konvergenzradius
Eine Potenzreihe konvergiert entweder nur für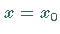 
oder für alle Werte von
,
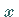oder es gibt eine Zahl 
,
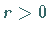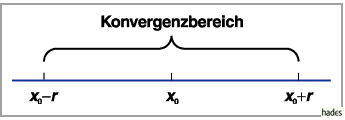
den Konvergenzradius (s. Abbildung), so
daß die Reihe für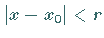 
absolut konvergiert und für
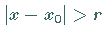divergiert.
Der Konvergenzradius kann mittels
 |
(7.77) |
bestimmt werden, falls die Grenzwerte existieren.
In den Endpunkten des Konvergenzintervalls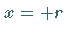 
und 
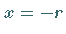für
die Reihe (7.76a) und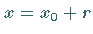 
und 
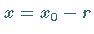für die
Reihe (7.76b) kann die Reihe entweder konvergent oder divergent sein.
Existieren diese Grenzwerte nicht, dann ist an Stelle des gewöhnlichen Limes (
)
der Limes superior 
zu nehmen (s. Lit. 7.10, Bd. I).
