|
|
|
|
| (7.6) |
| Beispiel | |
|
Von den Folgen in den Beispielen A bis J sind
konvergent:
die Folge in C mit | |
3. Divergenz einer Zahlenfolge:
Nichtkonvergente Zahlenfolgen heißen divergent .
Man spricht von bestimmter Divergenz , wenn ![]() mit unbegrenzt wachsendem
mit unbegrenzt wachsendem
![]() nach der positiven oder negativen Seite jede vorgegebene Zahl von beliebig
großem Betrag überschreitet.
Man schreibt dann:
nach der positiven oder negativen Seite jede vorgegebene Zahl von beliebig
großem Betrag überschreitet.
Man schreibt dann:
| (7.7) |
| Beispiel A | |
|
Von den Folgen in den Beispielen A bis J sind
die Folgen A und B gegen | |
| Beispiel B | |
|
Von den Folgen in den Beispielen A bis J ist die Folge D unbestimmt divergent. | |
4. Sätze über Grenzwerte von Zahlenfolgen:
a) Wenn die Folgen ![]() und
und ![]() konvergieren, gilt
konvergieren, gilt
| (7.8) |
| (7.9) |
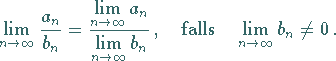 |
(7.10) |
| (7.11) |
|
|
|