|
|
|
|
| (6.65a) |
| (6.65b) |
| (6.66a) |
| (6.66b) |
| (6.66c) |
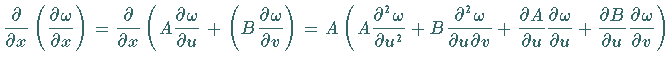 |
|||
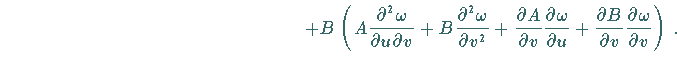 |
(6.67) |
| Beispiel | |||||||
|
Der LAPLACE-Operator soll in
Polarkoordinaten ausgedrückt werden:
Gang der Rechnung:
| |||||||
Hinweis: Wenn Funktionen mit mehreren Veränderlichen substituiert werden sollen, können ähnliche Substitutionsformeln hergeleitet werden.
|
|
|