Partielle Ableitung 2. Ordnung
Die partielle Ableitung 2. Ordnung einer Funktion
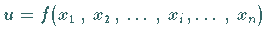 kann sowohl nach der gleichen Variablen gebildet werden, wie die erste Ableitung, d.h.
kann sowohl nach der gleichen Variablen gebildet werden, wie die erste Ableitung, d.h.
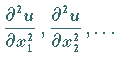 ,
als auch nach einer anderen Variablen, d.h.
,
als auch nach einer anderen Variablen, d.h.
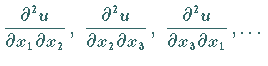 .
Im zweiten Falle spricht man von einer gemischten Ableitung.
Der Wert einer gemischten Ableitung ist für gegebene Werte von
.
Im zweiten Falle spricht man von einer gemischten Ableitung.
Der Wert einer gemischten Ableitung ist für gegebene Werte von 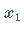 und
und 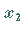 unabhängig von der Reihenfolge der Ableitungsbildung, wenn die gemischte Ableitung
in dem betrachteten Punkt stetig ist.
Man spricht vom SCHWARZschen Vertauschungssatz :
unabhängig von der Reihenfolge der Ableitungsbildung, wenn die gemischte Ableitung
in dem betrachteten Punkt stetig ist.
Man spricht vom SCHWARZschen Vertauschungssatz :
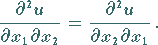 |
(6.45) |
Partielle Ableitungen höherer Ordnung, wie z.B.
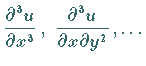 sind analog definiert.
sind analog definiert.
![]() kann sowohl nach der gleichen Variablen gebildet werden, wie die erste Ableitung, d.h.
kann sowohl nach der gleichen Variablen gebildet werden, wie die erste Ableitung, d.h.
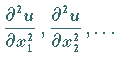 ,
als auch nach einer anderen Variablen, d.h.
,
als auch nach einer anderen Variablen, d.h.
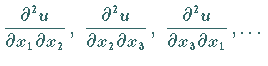 .
Im zweiten Falle spricht man von einer gemischten Ableitung.
Der Wert einer gemischten Ableitung ist für gegebene Werte von
.
Im zweiten Falle spricht man von einer gemischten Ableitung.
Der Wert einer gemischten Ableitung ist für gegebene Werte von ![]() und
und ![]() unabhängig von der Reihenfolge der Ableitungsbildung, wenn die gemischte Ableitung
in dem betrachteten Punkt stetig ist.
Man spricht vom SCHWARZschen Vertauschungssatz :
unabhängig von der Reihenfolge der Ableitungsbildung, wenn die gemischte Ableitung
in dem betrachteten Punkt stetig ist.
Man spricht vom SCHWARZschen Vertauschungssatz :
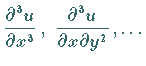 sind analog definiert.
sind analog definiert.