Verallgemeinerter Mittelwertsatz der Differentialrechnung
Wenn zwei Funktionen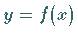 
und 
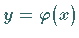in einem abgeschlossenen Intervall
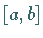stetig sind und wenigstens im Innern Ableitungen besitzen, wobei 
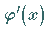an
keiner Stelle des Intervalls verschwinden darf, dann existiert zwischen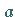 
und 
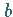wenigstens eine Zahl 
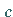derart, daß die Gleichung gilt
 |
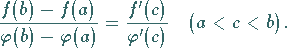(6.32) |
Die geometrische Bedeutung des verallgemeinerten Mittelwertsatzes entspricht der des
gewöhnlichen Mittelwertsatzes.
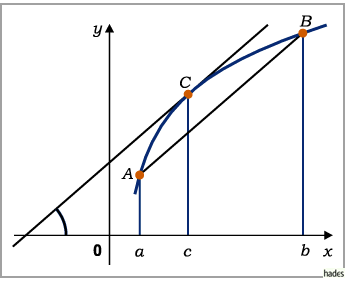
Geht man z.B. davon aus, daß die Kurve in der Abbildung in der Parameterform
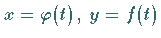gegeben ist, wobei die Punkte 
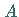und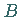 
den
Parameterwerten 
bzw. 
entsprechen sollen, dann gilt für den Punkt 
 |
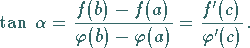(6.33) |
Fü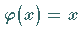r 
geht der verallgemeinerte Mittelwertsatz in den
gewöhnlichen Mittelwertsatz über.
