Nach einem Theorem von CARTAN kann in einer halbeinfachen LIE-Algebra
der Dimension 
durch die Transformation
 |
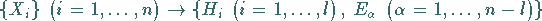(5.153) |
eine spezielle Basis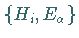 
( CARTAN-WEYL-Basis, Standardbasis)
so eingeführt werden, daß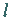 
linear unabhängige, miteinander kommutierende
Operatoren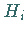 
 |
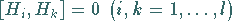(5.154) |
eine Unteralgebra aufspannen.
Die Zahl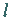
wird als Rang der LIE-Algebra ( LIE-Gruppe) bezeichnet.
Die Operatoren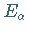 
spannen die Teilalgebra der Dimension 
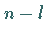auf.
Sie kommutieren weder untereinander noch mit den Basiselementen 
.
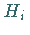Z.B. gilt:
 |
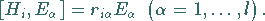(5.155) |
Die reellen Zahlen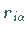 
lassen sich zu einem Vektor 
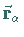(Wurzelvektor) in einem 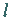-dimensionalen Raum zusammenfassen:
 |
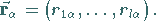(5.156) |
Das System der Wurzelvektoren kann benutzt werden, um die möglichen
LIE-Algebren zu klassifizieren.
Da zu jeder Darstellung der LIE-Algebra eine Darstellung der entsprechenden
lokalen LIE-Gruppe gehört, genügt es, Darstellungen der LIE-Algebra
zu finden, um zu einer Klassifizierung der Darstellungen der LIE-Gruppe zu
kommen.
