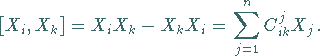Die infinitesimalen Generatoren 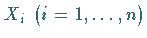 einer
LIE-Gruppe bilden die Basis eines
einer
LIE-Gruppe bilden die Basis eines  -dimensionalen linearen Raumes,
der zur LIE-Algebra
-dimensionalen linearen Raumes,
der zur LIE-Algebra 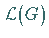 wird, wenn man ihn durch
Linearkombinationen
wird, wenn man ihn durch
Linearkombinationen 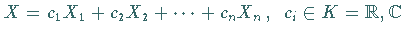 und Kommutatorbildung
und Kommutatorbildung 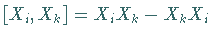 abschließt.
abschließt.
Der Kommutator zweier Generatoren ist als Linearkombination der Generatoren
darstellbar:
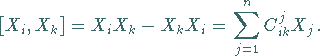 |
(5.146) |
Die Koeffizienten 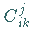 sind die Strukturkonstanten der LIE-Algebra
sind die Strukturkonstanten der LIE-Algebra
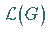 .
Bei einer Basistransformation in
.
Bei einer Basistransformation in 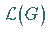 transformieren sie sich wie
Tensoren 3. Stufe.
transformieren sie sich wie
Tensoren 3. Stufe.