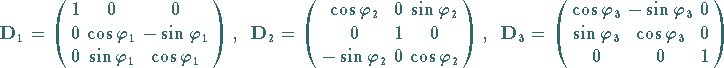Die Matrizen
 |
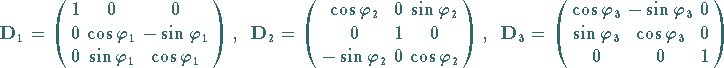(5.136) |
vermitteln die Transformation eines Ortsvektors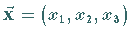 
des dreidimensionalen Raumes bei Drehungen mit dem Drehwinkel 
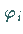um
die Achse 
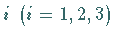eines kartesischen Koordinatensystems.
Alle dreidimensionalen Drehungen (eigentliche Drehungen ohne Inversion) bilden die
dreiparametrige spezielle orthogonale Gruppe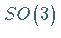 
;
zweidimensionale Drehungen
sind eine einparametrige ABELsche Untergruppe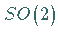 
von .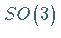
Eine Entwicklung der trigonometrischen Funktionen in den Matrixelementen von
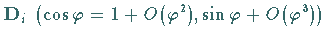ergibt für infinitesimale Drehungen 
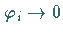eine
Liniearisierung der Transformation nach
 |
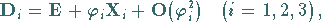(5.137) |
wobei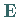 
die dreidimensionale Einheitsmatrix bezeichnet, 
eine
Matrix mit Elementen mindestens der Ordnung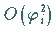 
und die Matrizen
 |
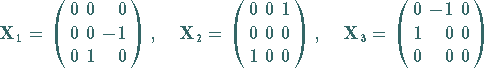(5.138) |
eine Darstellung der infinitesimalen Generatoren der LIE-Gruppe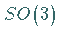 
liefern.
Die Elemente der lokalen LIE-Gruppe sind die Matrizen
 |
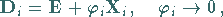(5.139) |
deren Elemente außerhalb der Hauptdiagonalen sich nur wenig von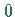 
unterscheiden.
Um zur globalen LIE-Gruppe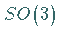
aller endlichen dreidimensionalen Drehungen
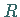zu gelangen, sind infinitesimale Drehungen wiederholt auszuführen:
 |
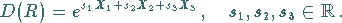(5.140) |
Anstelle der Parameter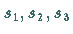 
können auch der Drehwinkel 
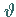und
die drei Komponenten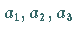 
eines Einheitsvektors 
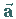in Richtung der
Drehachse durch den Koordinatenursprung eingeführt werden, um das Element der
Drehgruppe zu bestimmen:
 |
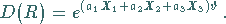(5.141) |
