|
|
|
|
werden oft Fuzzy-Mengen verwendet,
die durch Dreieckfunktionen dargestellt, die sich auf der Höhe 0,5 schneiden werden.
Solche Fuzzy-Mengen genügen drei Bedigungen:
gibt es eine Eingabe 
für die nur eine
Regel erfüllt ist.
Für diese Eingabe 
wird die Ausgabe über 
berechnet.
Dadurch ist die Ausgabe des Fuzzy-Systems an 
Stützstellen 
festgelegt.
Man kann daher sagen, das Fuzzy-System interpoliert die Stützstellen .
Die Forderung, daß an den Stützstellen
nur die eine Regel
gilt,
ist für eine exakte Interpolation hinreichend, aber nicht notwendig.
Für zwei Regeln 
und 
,
wie sie im folgenden betrachtet werden,
bedeutet diese Forderung, daß 
gilt.
Zur Erfüllung der 1. Bedingung muß
sein.
Das ist eine hinreichende Bedingung für eine exakte Interpolation der Stützstellen.
und 
zwei solche Stützstellen mit den Regeln
und
so berechnet sich für Eingaben 
die Ausgabe 
zu
 |
(5.413) |
mit von 
abhängigen 
und 
sowie
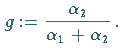
Der eigentliche Verlauf der Interpolationskurve zwischen
und
wird von der
Funktion 
bestimmt.
Diese wird daher als Kurvenverlauf bezeichnet.
Sie hängt nur von den Erfüllungsgraden 
und
ab, die sich als
Werte der Zugehörigkeitsfunktionen 
und 
an der Stelle
ergeben, d.h., es ist 
und
oder kurz 
und
Der Kurvenverlauf hängt nur vom Verhältnis 
der
Zugehörigkeitsfunktionen ab.
3. Die Zugehörigkeitsfunktionen sind positiv, so daß die Ausgabe
eine
Konvexkombination der Konklusionen
ist.
Daher gilt:
 |
(5.414) |
bzw. für den allgemeinen Fall
 |
(5.415) |
Für konstante Konklusionen bewirken die Terme 
und 
lediglich eine
Verschiebung und Streckung des Kurvenverlaufes 
Sind die Konklusionen von den Eingangsvariablen abhängig, dann wird der Kurvenverlauf
in verschiedenen Abschnitten unterschiedlich verzerrt.
Dadurch kann sich eine andere Ausgangsfunktion ergeben.
Verwendet man für die Eingabe
linear abhängige Konklusionen und
Zugehörigkeitsfunktionen mit konstanter Summe, dann ist die Ausgabe
mit von
abhängigen 
und
einer Konstanten 
,
so daß sich Polynome 2. Ordnung als Interpolationsfunktionen
ergeben.
Diese Polynome kann man zur Konstruktion eines Interpolationsverfahrens mit Polynomen
2. Ordnung verwenden.
Allgemein ergibt sich aus der Wahl von Polynomen 
-ter Ordnung als Konklusion ein
Interpolationspolynom 
-ter Ordnung.
Daher können die konventionellen Interpolationsverfahren, die lokal mit Polynomen
interpolieren (beispielsweise mit Splines), auch mit diesen Fuzzy-Systemen durchgeführt
werden.
|
|