Modellierung fuzzy-wertiger Relationen
Unscharfe oder fuzzy-wertige Relationen wie beispielsweise ,,ungefähr gleich``,
,,im wesentlichen grösser`` oder ,,im wesentlichen kleiner`` etc.
spielen für die praktischen Anwendungen eine große Rolle.
Sie werden als Relationen zwischen Zahlen und demzufolge als Teilmengen im 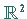 erklärt.
So läßt sich Gleichheit ,,=`` als Menge
erklärt.
So läßt sich Gleichheit ,,=`` als Menge
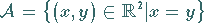 |
(5.375) |
erklären, d.h. durch eine Gerade 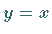 im
im 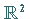 .
.
Zur Modellierung der Relation 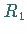 ,,ungefähr gleich`` kann angrenzend an ein
scharfes Gebiet (hier beschrieben durch die Gerade im
,,ungefähr gleich`` kann angrenzend an ein
scharfes Gebiet (hier beschrieben durch die Gerade im 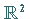 ,
allgemein im
,
allgemein im 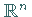 ,
mit der Toleranz
,
mit der Toleranz 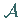 ) eine unscharfe Übergangszone zugelassen und verlangt
werden, daß die Zugehörigkeitsfunktion in einer gewünschten Art (linear oder
quadratisch) mit abnehmender Zugehörigkeit gegen Null geht.
Eine lineare Abnahme kann wie folgt modelliert werden:
) eine unscharfe Übergangszone zugelassen und verlangt
werden, daß die Zugehörigkeitsfunktion in einer gewünschten Art (linear oder
quadratisch) mit abnehmender Zugehörigkeit gegen Null geht.
Eine lineare Abnahme kann wie folgt modelliert werden:
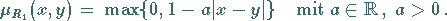 |
(5.376) |
Zur Modellierung der Relation 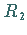 ,,im wesentlichen größer als``
ist es zweckmäßig, von der scharfen Relation ,,
,,im wesentlichen größer als``
ist es zweckmäßig, von der scharfen Relation ,,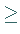 `` auszugehen.
Die zugehörige Wertemenge ist dann gegeben durch
`` auszugehen.
Die zugehörige Wertemenge ist dann gegeben durch
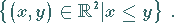 |
(5.377) |
Sie beschreibt das scharfe Gebiet oberhalb der Geraden 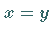 .
Die Modellierung ,,im wesentlichen`` bedeutet, daß geringe Unterschreitungen
in ein Randgebiet unterhalb der Halbebene, gekennzeichnet durch die Gerade, noch
akzeptiert werden.
Die Modellierung von
.
Die Modellierung ,,im wesentlichen`` bedeutet, daß geringe Unterschreitungen
in ein Randgebiet unterhalb der Halbebene, gekennzeichnet durch die Gerade, noch
akzeptiert werden.
Die Modellierung von 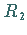 ergibt sich dann zu
ergibt sich dann zu
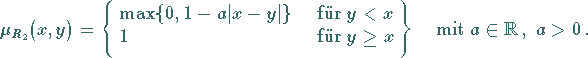 |
(5.378) |
Setzt man für eine der Variablen einen festen Wert ein, z.B. 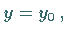 dann folgt
aus dieser modellmäßigen Beschreibung unmittelbar, daß
dann folgt
aus dieser modellmäßigen Beschreibung unmittelbar, daß 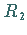 als unscharfe
Schranke bezüglich der anderen Variablen interpretiert werden kann.
Unscharfe Schranken besitzen im Bereich der unscharfen mathematischen Optimierung, der
qualitativen Datenanalyse und der Musterklassifikation praktische Bedeutung.
als unscharfe
Schranke bezüglich der anderen Variablen interpretiert werden kann.
Unscharfe Schranken besitzen im Bereich der unscharfen mathematischen Optimierung, der
qualitativen Datenanalyse und der Musterklassifikation praktische Bedeutung.
Die vorstehende Betrachtung zeigt, daß das Konzept der unscharfen Relationen, d.h.
der unscharfen Beziehungen zwischen mehreren Objekten, mit Hilfe unscharfer Mengen
aufgebaut werden kann.
Im folgenden werden Grundtatsachen zweistelliger Relationen über einem Grundbereich
behandelt, dessen Elemente geordnete Paare sind.
![]() ,,im wesentlichen größer als``
ist es zweckmäßig, von der scharfen Relation ,,
,,im wesentlichen größer als``
ist es zweckmäßig, von der scharfen Relation ,,![]() `` auszugehen.
Die zugehörige Wertemenge ist dann gegeben durch
`` auszugehen.
Die zugehörige Wertemenge ist dann gegeben durch
![]() .
Die Modellierung ,,im wesentlichen`` bedeutet, daß geringe Unterschreitungen
in ein Randgebiet unterhalb der Halbebene, gekennzeichnet durch die Gerade, noch
akzeptiert werden.
Die Modellierung von
.
Die Modellierung ,,im wesentlichen`` bedeutet, daß geringe Unterschreitungen
in ein Randgebiet unterhalb der Halbebene, gekennzeichnet durch die Gerade, noch
akzeptiert werden.
Die Modellierung von ![]() ergibt sich dann zu
ergibt sich dann zu
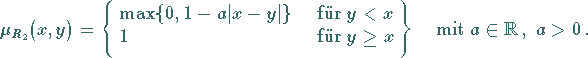
![]() dann folgt
aus dieser modellmäßigen Beschreibung unmittelbar, daß
dann folgt
aus dieser modellmäßigen Beschreibung unmittelbar, daß ![]() als unscharfe
Schranke bezüglich der anderen Variablen interpretiert werden kann.
Unscharfe Schranken besitzen im Bereich der unscharfen mathematischen Optimierung, der
qualitativen Datenanalyse und der Musterklassifikation praktische Bedeutung.
als unscharfe
Schranke bezüglich der anderen Variablen interpretiert werden kann.
Unscharfe Schranken besitzen im Bereich der unscharfen mathematischen Optimierung, der
qualitativen Datenanalyse und der Musterklassifikation praktische Bedeutung.