Glockenförmige Zugehörigkeitsfunktionen

Resümee: Als Resümee der zu betrachtenden Beispiele ergibt sich, daß unscharfe und unpräzise Informationen durch Fuzzy-Mengen beschrieben und durch Zugehörigkeitsfunktionen visualisiert werden können. Sprachliche Aussagen wie WENN-DANN-Regeln werden dann zu Berechnungsverfahren.

Beispiel A
	Eine Klasse glockenförmiger, differenzierbarer Zugehörigkeitsfunktionen erhält man mit Hilfe von Fun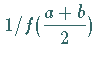ktionen der Art (5.349) wenn geeignet wählt wird. Für und z.B. bzw.  oder erhält man mit dem Normierungsfaktor die in der folgenden Abbildung dargestellten Zugehörigkeitsfunktionen 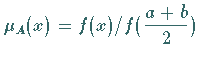unterschiedlicher Breite einer symmetrischen Kurvenschar. Mit dem Wert ergibt sich die äußere, mit die innere Kurve.

Asymmetrische Zugehörigkeitsfunktionen in wie sie die folgende Abbildung zeigt, erhält man beispielsweise für oder mit geeigneten Normierungsfaktoren. Der Faktor im ersten Polynom bewirkt eine Verschiebung des Maximums nach links und liefert eine asymmetrische Kurvenform. Entsprechend bewirkt der Faktor im zweiten Polynom eine Verschiebung nach rechts mit asymmetrischer Form.

Beispiel B

Beispiele für eine noch flexiblere Klasse von Zugehörigkeitsfunktionen erhält man durch eine Transformation in gemäß (5.350) wobei für die bereits bei den glockenförmigen Zugehörigkeitsfunktionen benutzte Funktion (5.349) mit verwendet werden kann. Ist eine glatte Transformation in [a,b], d.h. ist unendlich differenzierbar im Intervall , so ist auch glatt, weil glatt ist. Verlangt man, daß steigend oder fallend und glatt ist, dann liefert die Transformation Möglichkeiten, die Kurvenform einer Zugehörigkeitsfunktion zu verändern. In der Praxis sind Polynome für die Transformation gut geeignet. Im Intervall ist das einfachste Polynom die Identität . Das nächst einfache Polynom mit den angegebenen Eigenschaften ist mit einer Konstanten . Mit der Wahl für maximale Krümmung des Polynoms ergibt sich . Wählt man für die Identitätsfunktion, d.h. so kann man zusammen mit rekursiv durch für weitere Polynome berechnen. Setzt man für die Transformation in (5.350) die entsprechenden Transformationspolynome ein, so erhält man eine Folge glatter Funktionen und (linke Abbildung), die zur Konstruktion von Zugehörigkeitsfunktionen verwendet werden können, wobei zu einer Geraden konvergiert. Mit Hilfe der Funktion sowie ihrer gespiegelten Form und einer waagerechten Geraden kann eine trapezförmige Zugehörigkeitsfunktion differenzierbar approximiert werden (rechte Abbildung).