Elementarkonjunktion, Elementardisjunktion
Es sei 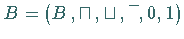 eine
BOOLEsche Algebra und
eine
BOOLEsche Algebra und 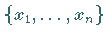 eine Menge BOOLEscher
Variabler.
Jede Konjunktion bzw. Disjunktion, in der jede Variable oder ihre Negation genau einmal
vorkommt, heißt Elementarkonjunktion bzw. Elementardisjunktion (in den
Variablen
eine Menge BOOLEscher
Variabler.
Jede Konjunktion bzw. Disjunktion, in der jede Variable oder ihre Negation genau einmal
vorkommt, heißt Elementarkonjunktion bzw. Elementardisjunktion (in den
Variablen 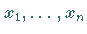 ).
).
Es sei 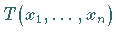 ein BOOLEscher Ausdruck.
Eine Disjunktion
ein BOOLEscher Ausdruck.
Eine Disjunktion 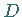 von Elementarkonjunktionen mit
von Elementarkonjunktionen mit  heißt
kanonisch disjunktive Normalform (KDNF) von
heißt
kanonisch disjunktive Normalform (KDNF) von 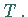 Eine Konjunktion
Eine Konjunktion 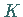 von Elementardisjunktionen mit
von Elementardisjunktionen mit 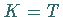 heißt
kanonisch konjunktive Normalform (KKNF) von
heißt
kanonisch konjunktive Normalform (KKNF) von 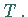
Um zu zeigen, daß sich jede BOOLEsche Funktion  durch einen BOOLEschen
Ausdruck darstellen läßt, wird zu der in der folgenden Tabelle gegebenen Funktion
durch einen BOOLEschen
Ausdruck darstellen läßt, wird zu der in der folgenden Tabelle gegebenen Funktion
 die KDNF konstruiert:
die KDNF konstruiert:
Die KDNF zur BOOLEschen Funktion  besteht aus den Elementarkonjunktionen
besteht aus den Elementarkonjunktionen
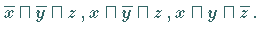 Diese Elementarkonjunktionen gehören zu den Belegungen
Diese Elementarkonjunktionen gehören zu den Belegungen 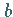 der Variablen, die bei
der Variablen, die bei  den Funktionswert 1 haben.
Ist in
den Funktionswert 1 haben.
Ist in 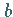 eine Variable
eine Variable 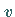 mit 1 belegt, so wird
mit 1 belegt, so wird 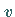 in die Elementardisjunktion
aufgenommen, andernfalls
in die Elementardisjunktion
aufgenommen, andernfalls 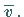 Für das obige Beispiel lautet die KDNF:
Für das obige Beispiel lautet die KDNF:
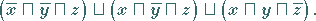 |
(5.327) |
Die ,,duale`` Form zur KDNF ist die KKNF:
Die Elementardisjunktionen gehören zu den Belegungen 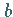 der Variablen, die bei
der Variablen, die bei  den Funktionswert 0 haben.
Ist in
den Funktionswert 0 haben.
Ist in 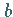 eine Variable
eine Variable 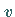 mit 0 belegt, so wird
mit 0 belegt, so wird 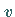 in die Elementardisjunktion
aufgenommen, andernfalls
in die Elementardisjunktion
aufgenommen, andernfalls 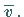 Somit lautet die KKNF für das obige Beispiel:
Somit lautet die KKNF für das obige Beispiel:
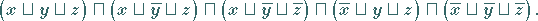 |
(5.328) |
Die KDNF und die KKNF zu  sind eindeutig bestimmt, wenn man eine Reihenfolge der
Variablen und eine Reihenfolge der Belegungen vorgibt, z.B. wenn man die Belegungen
als Dualzahlen auffaßt und der Größe nach ordnet.
sind eindeutig bestimmt, wenn man eine Reihenfolge der
Variablen und eine Reihenfolge der Belegungen vorgibt, z.B. wenn man die Belegungen
als Dualzahlen auffaßt und der Größe nach ordnet.
![]() der Variablen, die bei
der Variablen, die bei ![]() den Funktionswert 0 haben.
Ist in
den Funktionswert 0 haben.
Ist in ![]() eine Variable
eine Variable ![]() mit 0 belegt, so wird
mit 0 belegt, so wird ![]() in die Elementardisjunktion
aufgenommen, andernfalls
in die Elementardisjunktion
aufgenommen, andernfalls ![]() Somit lautet die KKNF für das obige Beispiel:
Somit lautet die KKNF für das obige Beispiel:
![]() sind eindeutig bestimmt, wenn man eine Reihenfolge der
Variablen und eine Reihenfolge der Belegungen vorgibt, z.B. wenn man die Belegungen
als Dualzahlen auffaßt und der Größe nach ordnet.
sind eindeutig bestimmt, wenn man eine Reihenfolge der
Variablen und eine Reihenfolge der Belegungen vorgibt, z.B. wenn man die Belegungen
als Dualzahlen auffaßt und der Größe nach ordnet.