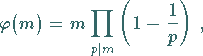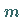|
|
|
|
mit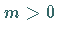 
kann man die Anzahl der zu
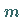teilerfremden
Zahlen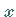 
mit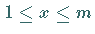 
angeben.
Die zugehörige Funkion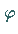 
wird EULERsche Funktion genannt.
Der Funktionswert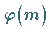 
ist die Anzahl der primen Restklassen modulo
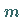(s. Prime Restklassen). 
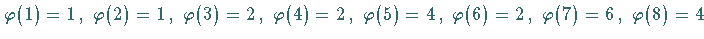usw.
Allgemein gilt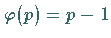 
für jede Primzahl 
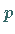und
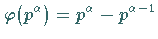für jede Primzahlpotenz 
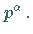Ist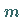
eine beliebige natürliche Zahl, dann kann man
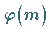wie folgt berechnen:
 |
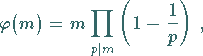(5.280a) |
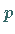von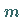
zu erstrecken ist.
| Beispiel | |
|
| |
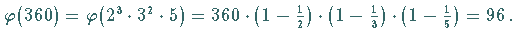
Außerdem gilt
 |
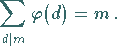(5.280b) |
,
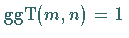dann ist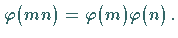 
| Beispiel | |
|
| |
|
|
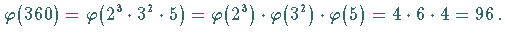
