Restklassen, Restklassenring
1. Restklassen modulo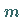 
:
Da die Kongruenz modulo
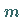eine Äquivalenzrelation in 
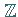ist, induziert diese
Relation eine Klasseneinteilung von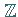
in Restklassen modulo m :
 |
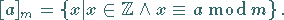(5.265) |
Die Restklasse ,,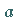
modulo 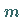`` besteht aus allen ganzen Zahlen, die bei
Division durch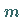
den gleichen Rest wie
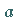lassen.
Es gilt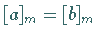 
genau dann, wenn 
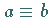mod
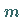ist.
Zum Modul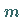
gibt es genau
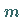Restklassen, zu deren Beschreibung man in der Regel ihre
kleinsten nichtnegativen Repräsentanten verwendet:
 |
(5.266) |
2. Restklassenaddition und Restklassenmultiplikation:
In der Menge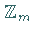 
der Restklassen modulo
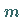wird durch
 |
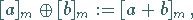(5.267) |
 |
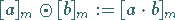(5.268) |
eine Restklassenaddition bzw. Restklassenmultiplikation erklärt.
Diese Restklassenoperationen sind unabhängig von der Auswahl der Repräsentanten, d.h.,
aus
 |
(5.269a) |
folgt
 |
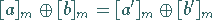(5.269b) |
und
 |
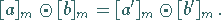(5.269c) |
3. Restklassenring modulo :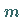
Die Restklassen modulo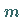
bilden bezüglich der Restklassenaddition und
Restklassenmultiplikation einen Ring mit Einselement, den
Restklassenring modulo m .
Ist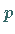 
eine Primzahl, dann ist der Restklassenring modulo
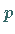ein
Körper.
