Ausdrücke des Prädikatenkalküls
Allgemein werden die Ausdrücke des Prädikatenkalküls wieder induktiv
definiert:
1. Sind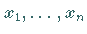 
Individuenvariable und 
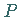eine 
-stellige
Prädikatenvariable, so ist
 |
(5.21a) |
2. Sind 
und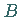 
Ausdrücke, so sind es auch
 |
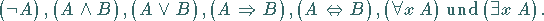(5.21b) |
Betrachtet man Aussagenvariable als nullstellige Prädikatenvariable, so erkennt man die
Aussagenlogik als Teil der Prädikatenlogik.
Eine Individuenvariable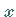 
kommt in einem Ausdruck gebunden vor, wenn
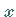Variable
eines Quantors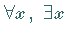 
ist oder im Wirkungsbereich eines Quantors
liegt; andernfalls kommt
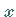in diesem Ausdruck frei vor.
Ein Ausdruck der Prädikatenlogik, der keine freien Variablen enthält, heißt
geschlossene Formel .
