|
Es ist die DIOPHANTische Gleichung
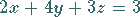 |
(5.262a) |
zu lösen.
Sie ist lösbar, denn 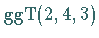 ist ein Teiler von 3.
ist ein Teiler von 3.
Die DIOPHANTische Gleichung
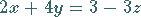 |
(5.262b) |
in den Unbekannten 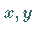 ist genau dann lösbar, wenn
ist genau dann lösbar, wenn 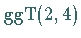 ein
Teiler von
ein
Teiler von 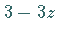 ist.
Die zugehörige DIOPHANTische Gleichung
ist.
Die zugehörige DIOPHANTische Gleichung 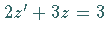 hat die Lösungsmenge
hat die Lösungsmenge
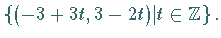 Daraus folgt
Daraus folgt 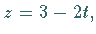 und gesucht ist nun die Lösungsmenge der lösbaren
DIOPHANTischen Gleichung
und gesucht ist nun die Lösungsmenge der lösbaren
DIOPHANTischen Gleichung 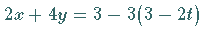 bzw.
bzw.
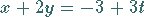 |
(5.262c) |
für jedes 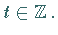
Die Gleichung (5.262c) ist lösbar wegen
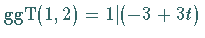 .
Es gilt .
Es gilt 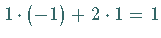 und
und 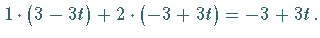 Die Lösungsmenge ist
Die Lösungsmenge ist 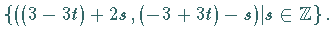 Daraus folgt
Daraus folgt 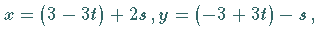 so daß sich die Lösungsmenge von
(5.262a) zu
so daß sich die Lösungsmenge von
(5.262a) zu 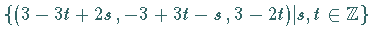 ergibt.
ergibt.
|