1. Allgemeiner Fall:
Eine Gleichung 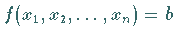 wird DIOPHANTische Gleichung in
wird DIOPHANTische Gleichung in
 Unbekannten genannt, wenn
Unbekannten genannt, wenn 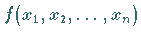 ein Polynom in
ein Polynom in
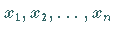 mit Koeffizienten aus der Menge
mit Koeffizienten aus der Menge 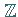 der ganzen Zahlen und
der ganzen Zahlen und 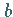 eine ganzzahlige Konstante ist und man sich ausschließlich für ganzzahlige
Lösungen interessiert.
Die Bezeichnung ,, DIOPHANTisch`` erinnert an den griechischen Mathematiker
DIOPHANT, der um 250 lebte.
eine ganzzahlige Konstante ist und man sich ausschließlich für ganzzahlige
Lösungen interessiert.
Die Bezeichnung ,, DIOPHANTisch`` erinnert an den griechischen Mathematiker
DIOPHANT, der um 250 lebte.
DIOPHANTische Gleichungen treten in der Praxis z.B. dann auf, wenn Beziehungen
zwischen Stückzahlen beschrieben werden.
Allgemein gelöst sind bisher nur die DIOPHANTischen Gleichungen bis zum zweiten
Grad mit zwei Variablen.
Für die DIOPHANTischen Gleichungen höheren Grades sind nur in Spezialfällen
Lösungen bekannt.
2. Lineare Diophantische Gleichungen in n Unbekannten:
Eine lineare DIOPHANTische Gleichung in  Unbekannten ist eine Gleichung
der Form
Unbekannten ist eine Gleichung
der Form
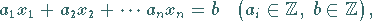 |
(5.259) |
für die nur die ganzzahligen Lösungen gesucht werden.
Im weiteren wird ein Lösungsverfahren angegeben.
3. Lösbarkeitsbedingung:
Unter der Bedingung, daß nicht alle 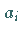 gleich 0 sind, ist die
DIOPHANTische Gleichung (5.259) genau dann lösbar, wenn der
gleich 0 sind, ist die
DIOPHANTische Gleichung (5.259) genau dann lösbar, wenn der
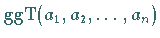 ein Teiler von
ein Teiler von 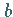 ist.
ist.
| Beispiel |
|
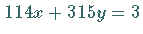 ist lösbar, denn
ist lösbar, denn 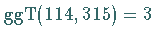 . .
|
Wenn eine lineare DIOPHANTische Gleichung in  Unbekannten (
Unbekannten (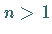 )
eine Lösung
hat und
)
eine Lösung
hat und 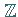 der Variablengrundbereich ist, so hat die Gleichung unendlich viele
Lösungen.
In der Lösungsmenge treten dann
der Variablengrundbereich ist, so hat die Gleichung unendlich viele
Lösungen.
In der Lösungsmenge treten dann 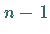 freie Parameter auf.
Für Teilmengen von
freie Parameter auf.
Für Teilmengen von 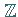 gilt dies aber nicht.
gilt dies aber nicht.
![]() Unbekannten (
Unbekannten (![]() )
eine Lösung
hat und
)
eine Lösung
hat und ![]() der Variablengrundbereich ist, so hat die Gleichung unendlich viele
Lösungen.
In der Lösungsmenge treten dann
der Variablengrundbereich ist, so hat die Gleichung unendlich viele
Lösungen.
In der Lösungsmenge treten dann ![]() freie Parameter auf.
Für Teilmengen von
freie Parameter auf.
Für Teilmengen von ![]() gilt dies aber nicht.
gilt dies aber nicht.